Учебно-методический комплекс по дисциплине «Теоретические основы автоматизированного управления», страница 58

Квадратические интегральные критерии качества управления. Такие критериизадаются следующими выражениями:

где t₁, t₂, ..., t_n - постоянные величины.

Критерии (5.4) - (5.6) называют обобщенными квадратическими критериями.

Γеометрический смысл интегрального квадратичного критерия J₂₀пояснен на рисунке 5.5. Выбирая параметры системы по минимуму квадратичного критерия J₂₀, приближаем кривую  к осям e и t. Методы вычисления этих оценок предложены А. И. Мандельштамом и Н. Д. Папалекси в 1909 г. В 1937 г. академик А. А. Харкевич применил эту оценку для исследования режимов работы усилителей, а в 1948 г. А. А. Красовский и А. А. Фельдбаум использовали ее для исследования качества линейных систем автоматического управления.

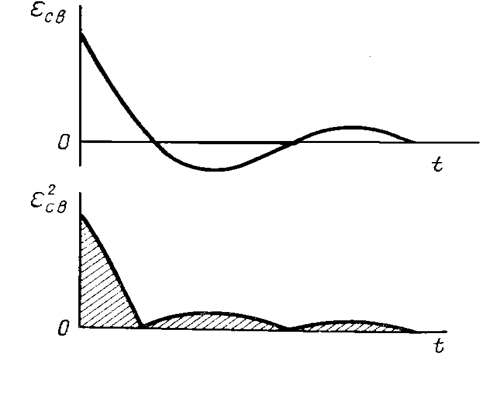
Рис. 5.5.

При выборе параметров системы по минимуму критерия J₂₀ часто получают нежелательную колебательность процесса, так как приближение процесса h(t) к идеальному скачку вызывает резкое увеличение начальной скорости, что, в свою очередь, может вызвать высокое перерегулирование, уменьшив при этом запас устойчивости. В обобщенных квадратичных критериях (5.4) - (5.6) накладывают ограничение не только на величину отклонения , но и на скорость отклонения  (в J₂₁), а также на производные второго, третьего и т. д. порядка в J₂₂,  ..., J_2n. Это означает приближение кривой не к ступенчатой функции, а к экспоненте в случае J₂₁ и к более плавной, но сложной кривой в случае использования J₂₂,  ..., J_2n. При выборе параметров САУ по минимуму критериев (5.4) - (5.6) существенен выбор постоянных времени t₁, ..., t_n, определяющих вес производных в этих критериях. Значительное увеличение t₁, ..., t_n приводит к отсутствию перерегулирования, но увеличивает время регулирования. При малых t₁, ..., t_n уменьшение колебательности процесса будет незначительным. Выбор t₁, ..., t_n осуществляется с учетом постоянной времени экстремали, к которой целесообразно приближать процесс.

Рассмотрим подробнее методику расчета САУ по минимуму обобщенного квадратичного критерия (5.5). Этот критерий можно представить в виде суммы двух интегралов

Если система устойчива, то тогда

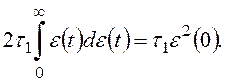
Кроме того, интеграл J₂₁ будет иметь минимально возможное значение

при

Если

то решение дифференциального уравнения (5.10)

является оптимальным переходным процессом, где t₁ - постоянная времени этого процесса.

При выборе параметров системы по минимуму J₂₁ обычно имеет место отклонение J^*_21min от наименьшего значения J_21min , т. е.

J^*_21min  - J_21min = d > 0.

А. А. Фельдбаум показал, что переходный процесс будет отличаться от экстремаль-ного на величину меньшую, чем  т. е.

По величине dможно оценить отклонение истинного переходного процесса  от экстремального (рис. 5.6). При увеличении порядка системы увеличивается и ширина зоны ± при этом уменьшается точность оценки качества системы (приближения переходного процесса к экстремали). Во избежание этого используют оценки вида (5.6). Величину t₁ задают по заданному времени регулирования t_p, т. е.

t_p /6 < t₁ < t_p /3.

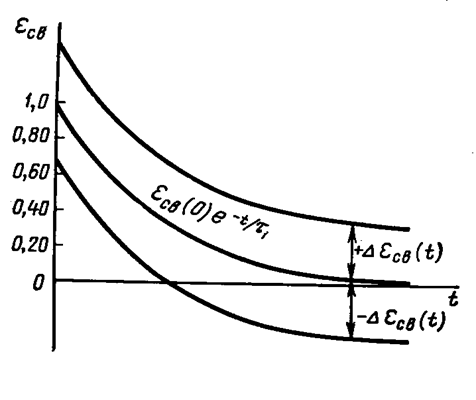
Рис. 5.6.

5.3. Статические и астатические САУ

Известна важная особенность САУ по отклонению: если в них использовать регуляторы, состоящих только из элементов, осуществляющих элементарные преобразования сигналов (сложение, вычитание, умножение, деление), то управление по отклонению может только уменьшить, а не устранить полностью погрешность функционирования системы. Такие САУ называют статическими.

В статических САУ величина установившейся погрешности управления зависит от величины возмущающего воздействия (нагрузки).

Примером стабилизирующей системы состатическим регулированием является генератор частотно модулированных сигналов с обратной связью по частоте (рис. 5.7).

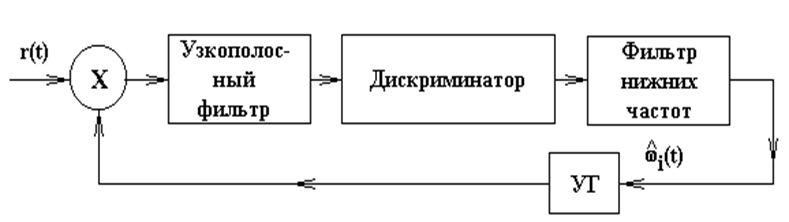
Рис. 5.7.