Учебно-методический комплекс по дисциплине «Теоретические основы автоматизированного управления», страница 65

Различают две группы критериев устойчивости: алгебраические и частотные. Критерии, которые позволяют определить, устойчива ли система, ограничиваясь лишь алгебраическими вычислениями над коэффициентами характеристического уравнения, называют алгебраическими критериями. К этим критериям относят критерий устойчивости Рауса и критерий устойчивости Гурвица. Рассматриваемые критерии для систем, описываемых уравнениями выше 4-й степени, дают лишь возможность определить, устойчива ли система при заданных численных значениях коэффициентов уравнения. Но их применение для определения изменения параметров системы с тем, чтобы сделать ее устойчивой, - затруднительно.

Частотный критерий устойчивости, впервые сформулированный Г. Найквистом, был применен для исследования устойчивости САУ А. В. Михайловым. Кроме того, им был сформулирован частотный критерий, получивший название критерия устойчивости Михайлова. Достоинством частотных характеристик являются наглядность и возможность использования частотных характеристик, полученных экспериментально, когда не известны дифференциальные уравнения системы или ее элементов. Частотные критерии могут быть разделены на две подгруппы.

1. Исследуется непосредственно замкнутая система (критерий устойчивости Михайлова). Этот критерий целесообразно применять тогда, когда размыкание системы не приводит к заметному упрощению задачи.

2. Об устойчивости замкнутой системы судят по частотным характеристикам разомкнутой системы (критерий устойчивости Найквиста). С помощью этого критерия наиболее просто анализировать запасы устойчивости САУ. Поэтому рассмотрим данный критерий.

Критерий устойчивости Найквиста. Этот критерий, разработанный американским ученым Г. Найквистом в 1932 г., позволяет судить об устойчивости замкнутой САУ по виду АФХ   разомкнутой системы (САУ с разомкнутой обратной связью). Для этого АФХ разомкнутой системы представляют в следующем виде:

где:

 и  - действительная и мнимая части АФХ;

 и  - модуль и фаза АФХ, связанные с  и  выражениями

Если изменять частоту  от 0 до ¥, то конец вектора  опишет в комплексной плоскости кривую, называемую АФХ разомкнутой системы (рис. 6.3). Вид этой кривой зависит от корней характеристического уравнения и, следовательно, по ней можно судить об устойчивости САУ.

Критерий устойчивости Найквиста можно сформулировать так: если разомкнутая САУ устойчива, то замкнутая САУ будет устойчива, если АФХ разомкнутой системы  не охватывает точку  комплексной плоскости.

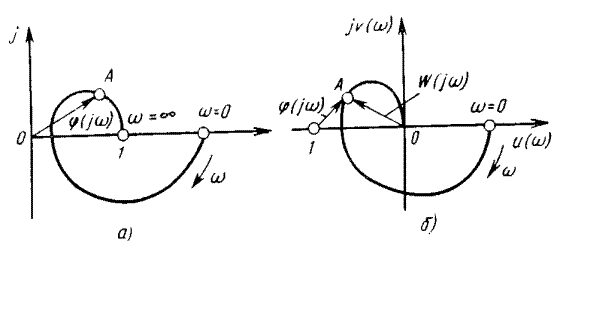
Рис. 6.3.

Во многих случаях указанные критерии устойчивости дают достаточное представление о качестве процесса управления. Формулировки этих критериев и доказательста их справедливости приведены в литературе по теории управления. Но математически все формы критериев устойчивости эквивалентны, так как все они определяют условия, при которых корни характеристического уравнения лежат в левой части комплексной плоскости. Поэтому здесь эти критерии рассматриваться не будут.

6.4. Запасы устойчивостиСАУ по модулю и фазе

Устойчивость замкнутой САР зависит от расположения годографа  АФХразомкнутой системы относительно критической точки с координатами . Чем ближе эта кривая проходит к критической точке, тем ближе замкнутая система к границе устойчивости.

Для устойчивых систем удаление годографа от критической точки  характеризуется запасом устойчивости по модулю и фазе (рис. 6.4). Минимальный отрезок действительной оси h, характеризующий расстояние между критической точкой и ближайшей точкой пересечения годографа с действительной осью, называют запасом устойчивости по модулю.

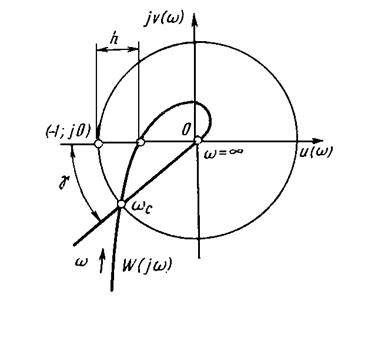
Рис. 6.4.