Учебно-методический комплекс по дисциплине «Теоретические основы автоматизированного управления», страница 17

где:

;   .

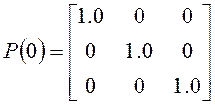Из сравнения уравнений (I) и (3.1) получим алгоритм вычисления вектора функций , входящих в уравнения формирования управляющего воздействия :

,

или (так как ):

.                                    (3.3)

Но из уравнений (6) и (7) видно, что

.               (3.4)

Поэтому из выражений (3.3) и (3.4) получим следующий алгоритм настройки параметров ПИ-регулятора:

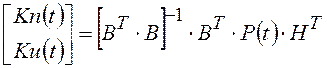.                                                         (3.5)

Результаты вычислений при  приведены на графиках изменения оценок параметров ПИ-регулятора:

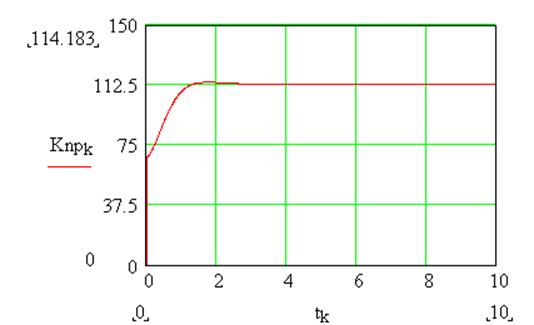
Рис.4. График изменения оценок параметра Kn

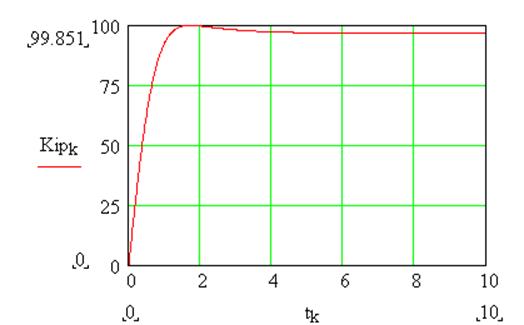
Рис.5. График изменения оценок параметра Ku

Из графиков видно, что получены состоятельные оценки параметров ПИ-регулятора. Окончательные значения оценок таковы: ;  .

5.  Анализ системы управления

по прямым показателям качества управления

Составим дискретную модель системы управления. Системе дифференциальных уравнений (b), (c), (d) соответствуют разностные уравнения:

;  (3.1)

;                                                                      (3.2)

     ;                                                           (3.3)

;   k=1, 2, …, N.                   (3.4)

В цикле по переменной  решить на ЭВМ систему уравнений (3.1)-(3.4), (5) с помощью математического пакета Mathcad.

Построить графики переходных процессов для управляемой переменной , требуемого закона изменения управляемой переменной ,  относительной погрешности управления 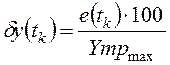 % и управляющего воздействия .

На рис. 6 приведен график изменения относительной погрешности управления.

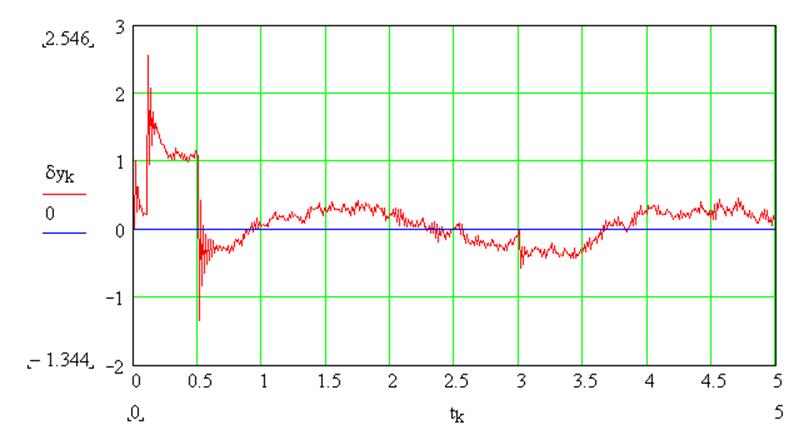
Рис.6. График изменения относительной погрешности управления

По графикам переходных процессов определить прямые показатели качества управления.

Вычислить среднее значение погрешности управления:

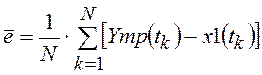
и среднее квадратическое значение погрешности управления за время управления:

.

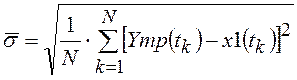5. Составить отчет по результатам выполнения задания.

4.  Материалы по промежуточному контролю знаний по дисциплине

  Контрольная работа №1

Вариант №1

1.  Изобразите схему САУ, реализующей принцип программного управления, и поясните реализацию этого принципа управления.

2.  Понятие "АЧХ". Алгоритм определения АЧХ по заданной передаточной функции.

3.  Определите передаточную функцию двух звеньев с передаточными функциям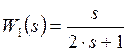и  и 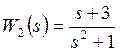, соединенных последовательно.

Вариант №2

1. Изобразите схему САУ, реализующей принцип управления по отклонению, и поясните реализацию этого принципа управления.

2. Понятие "ФЧХ". Алгоритм определения ФЧХ по заданной передаточной функции.

3. Определите передаточную функцию системы, изображенной на рисунке, где передаточная функция .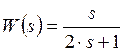

Вариант №3

1. Изобразите схему САУ, реализующей принцип управления по возмущению, и поясните реализацию этого принципа управления.

2. Алгоритм определения передаточной функции системы, образованной параллельным соединением звеньев.

3. САУ имеет математическую модель

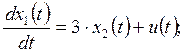
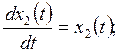
Выполните анализ управляемости САУ.

Вариант №4

1. Изобразите схему САУ, реализующей принцип комбинированного управления, и поясните реализацию этого принципа управления.

2.  Изобразите схему системы, образованной последовательным соединением звеньев. Алгоритм определения передаточной функции этой системы.

3. САУ имеет математическую модель

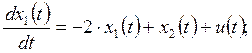
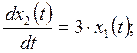
Выполните анализ наблюдаемости САУ.

Вариант №5

1. Математическая модель апериодического звена.

2. Изобразите схему системы, образованной соединением звеньев с обратной связью. Алгоритм определения передаточной функции этой системы.

3. Составьте передаточную функцию САУ, которая имеет математическую модель

.

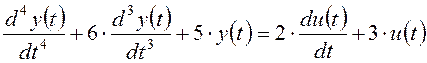Вариант №6

1. Понятие "передаточная функция системы".

2. Понятие "устойчивая система".

3. САУ имеет математическую модель

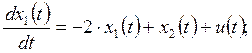
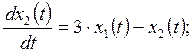
Выполните анализ управляемости САУ.

Вариант №7

1. Алгоритм определения характеристического уравнения по заданному дифференциальному уравнению.

2. Математическая модель пропорционального звена.

3. САУ имеет математическую модель

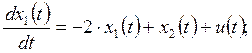
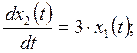
Выполните анализ наблюдаемости САУ.

Вариант №8