Учебно-методический комплекс по дисциплине «Теоретические основы автоматизированного управления», страница 36

2.1. Методика составления математического описания процессов,                                    протекающих в элементах САУ

Математическое описание составляют на основании тех физических законов, которые определяют протекание процессов в изучаемом элементе. Чаще всего исходными являются законы сохранения вещества и энергии.

Первым шагом при составлении математического описания изучаемого звена САУ является выявление физических процессов, протекающих в этом элементе. Математическое выражение соответствующего физического закона, который описывает этот процесс, является исходным дифференциальным уравнением звена.

Вторым шагом является определение факторов, от которых зависят переменные, входящие в исходное уравнение, и установление выражений, характеризующих эту зависимость. При этом уравнение звена нужно составить так, чтобы оно выражало зависимость между входными и выходными сигналами данного звена, т.е. между теми величинами, которые представляют воздействие данного звена на последующее звено и воздействие предыдущего звена на данное. Звено может иметь не одну входную величину, а несколько (например, при наличии дополнительных обратных связей). Кроме входных и выходной величин звено может иметь внешнее возмущающее воздействие.

В общем случае процессы, протекающие в произвольном элементе САУ, можно описать системой нелинейных дифференциальных уравнений первого порядка или одним нелинейным дифференциальным уравнением более высокого порядка. Для примера рассмотрим звено (рис. 2.1), физические процессы в котором можно описать дифференциальным уравнением второго порядка

где:

 y(t) - выходной сигнал звена,

 u(t), w(t) - входные сигналы звена,

 t - время.

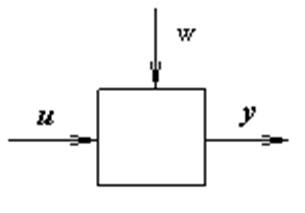
Рис. 2.1.

Уравнение (2.1), описывающее процессы в звене при произвольных входных сигналах, называют уравнением динамики звена.

Если входные сигналы принимают постоянные значения  u(t) = u₀ и w(t) = w₀, то с течением времени выходной сигнал звена примет постоянное значение y(t) = y₀. Тогда уравнение (2.1) примет вид

Уравнение (2.2) описывает установившийся, или статический режим, и его называют уравнением статики. Геометрические отображения уравнений статики (кривые, построенные в координатах y₀, u₀, w₀) называют статическими характеристиками. Статические характеристики звена (или САУ в целом) можно получить экспериментально путем исследования этого звена (или САУ) на специальном стенде в разных установившихся режимах.

2.2. Линеаризация дифференциальных уравнений звеньев САУ

Для упрощения расчетов нелинейные уравнения (2.1), (2.2) следует, когда это возможно, линеаризировать, т. е. заменить исходные нелинейные уравнения линейными, приближенно описывающими процессы, протекающие в изучаемом звене, для небольшого диапазона изменения входных и выходных сигналов относительно их значений, соответствующих требуемому (заданному) режиму работы САУ. В нормально работающей автоматической системе отклонение входных и выходных сигналов входящих в нее звеньев от требуемых (заданных) значений малы по величине, что позволяет произвести линеаризацию.

Достаточными признаками для проведения линеаризации обычно являются отсутствие разрывных, неоднозначных или резко изменяющихся характеристик и справедливость уравнения в течение всего интервала времени регулирования.

Линеаризацию дифференциальных уравнений выполняют при помощи формулы Тейлора. Используя последнюю, можно разложить нелинейную функцию нескольких переменных в ряд Тейлора - по степеням малых приращений этих переменных, которые берутся в окрестностях их значений, соответствующих установившемуся режиму. Формула Тейлора содержит остаточный член, исследование которого позволяет оценить величину погрешности, при учете только первых членов разложения.

Например, линеаризацию уравнения (2.1) можно осуществить следующим образом.

Обозначим отклонения  реальных значений , , , , ,  от требуемых , , , , , , соответствующих заданному режиму работы САУ, следующим образом: ,, , , ,.

Тогда