Учебно-методический комплекс по дисциплине «Теоретические основы автоматизированного управления», страница 44

y₁ = W₁×y_o,  y₂ = W₂×y_o, ...,  y_n = W_n×y_o.

Сложив эти уравнения и учитывая, что y = 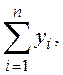 получим искомую формулу.

3. Звено, охваченное обратной связью (рис. 2.8). Принято считать, что звено охвачено обратной связью, если его выходной сигнал через какое-либо другое звено подается на вход. При этом если сигнал y₁ обратной связи вычитается из входного воздействия y_o (е₁ = y_o - y₁), то обратную связь называют отрицательной. Если сигнал y₁ обратной связи складывается с входным воздействием y_o (е₁ = y_o + y₁), то обратную связь называют положительной.

Разомкнем обратную связь перед сравнивающим звеном (рис. 2.8, а). Тогда получим цепь из двух последовательно соединенных звеньев. Поэтому передаточная функция W разомкнутой цепи (рис.2.8, а) равна произведению передаточной функции W_n прямой цепи и передаточной функции W_oc обратной связи: W = W_n×W_o.c.

Передаточная функция W_з замкнутой цепи с отрицательной обратной связью - звена, охваченного отрицательной обратной связью, - равна передаточной функции прямой цепи, деленной на единицу плюс передаточная функция разомкнутой цепи:

W₃ = W_n /(1 + W).

Для вывода этой формулы выпишем уравнения для каждого звена:

y = W_n×e₁;  y₁ = W_o.c×y,  e₁ = y_o - y₁.

В этой системе последнее уравнение - уравнение сравнивающего звена - называют уравнением замыкания.

Исключив переменные e₁ и y₁ из приведенной системы, получим уравнение

y = W_n×(y_o - Wo_.cy) или (1 + W_n ×W_o.c) y = W_n ×y_o.

Отсюда

W₃ = y/ y_o = W_n/(1 + W_n ×W_oc) = W_n/(1 + W).

Если обратная связь положительна, то аналогично получим

W₃ = y/y_o = W_n /(1 - W).

Передаточная функция разомкнутой цепи с положительной обратной связью равна передаточной функции прямой цепи, деленной на единицу минус передаточная функция разомкнутой цепи. Если передаточная функция W_oc = 1, то обратная связь называется единичной и структурная схема изображается так, как показано на рисунке 2.8, в. Передаточная функция W₃ при этом принимает вид W₃ = W_n/(1 - W_n) - при положительной обратной связи.

При преобразовании структурных схем возникает необходимость переноса и перестановки сумматоров и узлов. Рассмотрим, какие изменения в схеме при этом нужно произвести.

4.Перенос сумматора (рис. 2.9). Легко показать, что при переносе сумматора по ходу сигнала необходимо добавить звено с передаточной функцией, равной передаточной функции звена, через которое переносится сумматор (рис. 2.9, а). Если он переносится против хода сигнала, то необходимо добавить звено с передаточной функцией, равной обратной передаточной функции звена, через которое переносится сумматор (рис. 2.9, б).

При переносе сумматора возникают неэквивалентные участки линии связи. Эти участки на рисунке 2.9 заштрихованы.

5.Перенос узла (рис. 2.10). При переносе узла также необходимо добавить звено.

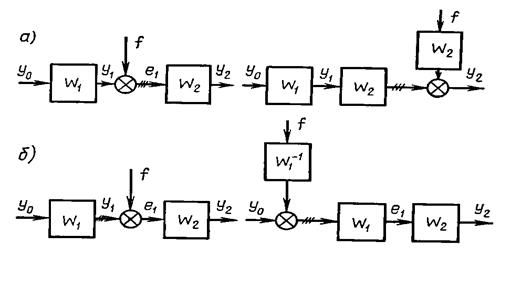
Рис. 2.9.

Если узел переносится по ходу сигнала, то добавляется звено с передаточной функцией, равной обратной передаточной функции звена, через которое переносится узел (рис. 2.10, б). Если узел переносится против хода сигнала, то добавляется звено с передаточной функцией, равной передаточной функции звена, через которое переносится узел (рис. 2.10,в).

6. Перестановка узлов и сумматоров (рис. 2.11). Узлы можно переставлять местами (рис. 2.19, а). Точно также можно переставлять сумматоры, не добавляя звена (рис. 2.11, б). При перестановке узла и сумматора (перенос узла через сумматор) необходимо добавить звено - суммирующее или сравнивающее (рис. 2.11, в, г). При переносе узла через сумматор, а также при перестановке сумматоров возникают неэквивалентные участки линии связи. Эти участки на рисунке заштрихованы.