а) нейтральный технологический прогресс в смысле Хиккса: такое изменение технологий, что при данной капиталовооруженности предельная норма технической замены капитала трудом остается неизменной. Данный тип технологического прогресса оставляет неизменным соотношение между объемами затрачиваемых факторов и может быть описан с использованием следующей производственной функции Y = eq×t×F(K, L), где q есть экзогенно задаваемый темп технологического прогресса,
б) нейтральный технологический прогресс в смысле Харрода: такое изменение технологий, что при данном уровне средней производительности капитала его предельная производительность остается неизменной. Данный тип технологического прогресса оставляет неизменным соотношение между выпуском и капиталом; при этом происходит рост капиталовооруженности и производительности живого труда. Он может быть описан с использованием следующей производственной функции Y=F(K, eq×t×L), где q есть экзогенно задаваемый темп технологического прогресса,
в) нейтральный технологический прогресс в смысле Солоу: такое изменение технологий, что при данном уровне средней производительности труда его предельная производительность остается неизменной. Данный тип технологического прогресса оставляет неизменным соотношение между выпуском и затратами труда, а капиталоемкость выпуска снижается. Он может быть описан с использованием следующей производственной функции Y=F(eq×t×K, L), где q есть экзогенно задаваемый темп технологического прогресса.
Только второй тип технологического прогресса совместим с равновесным ростом в модели Солоу: когда растет капиталовооруженность и производительность живого труда. Чтобы учесть это в модели требуется несколько модифицировать используемую производственную функцию. Именно, перейдем к следующей формализации:
Y =F(K, AL)
где переменная AL - носит название эффективного труда и измеряется, как это принято говорить, в единицах эффективного труда. При этом запись AL означает:
AL= A×L=(A0×eq×t)×L= (A0×eq×t)×(L0×el×t)= A0 L0×e(q+l)×t
где A=A0×eq×tесть функция усложнения труда, A0 - начальный уровень сложности живого труда, относящийся к базовому году, имеющему индекс 0, L0- объем живого в базовом году, q и l - соответственно темп технологического прогресса и темп прироста живого труда. Величину A0 вполне можно выбрать равной единице, что приводит к записи, использованной при определении нейтрального технологического прогресса по Харроду. Использование функции A позволяет провести редукцию труда, т.е. сведение живого труда к неким абстрактным единицам эффективного труда, т.е. живого труда той квалификации, которая имела место в базовом году[23].
Очевидно, что фактор эффективного труда растет с годовым темпом прироста равным q+l. Его использование в модели Солоу вместо фактора живого труда приводит к следующему соотношению:
dk/dt = s×f(k) - (d+l+q)×k,
однако смысл величин y=f(k) и k меняется. Теперь это уже есть отношения не живому труду, а к эффективному:
y=Y/AL=f(k)=F(K/AL, 1)
k=K/AL
в отличие от отношений к живому труду, которые мы теперь будем обозначать несколько по-другому - с индексом l:
yl=Y/L
kl=K/L
Оптимальные значения капиталовооруженности и душевого дохода, соответствующие траектории равновесного роста, находятся следующим образом:
s×f(k*) = (d+l+q)×k*
y*=f(k*)
где y* и k* - оптимальные значения дохода, отнесенного к эффективному труду, и капиталовооруженности эффективного труда. Переменные душевого дохода и капиталовооруженности живого труда, соответствующие стационарной траектории - yl* и kl*, уже не постоянные величины, как раньше, а функции от времени. Для траекторий равновесного роста выполняются следующие соотношения:
k*=const
y*=const
kl*= kl*(0)×eq×t
yl*(t)= yl*(0)×eq×t
K*(t)= K*(0)×e(l+q)×t
Y*(t)= Y*(0)×e(l+q)×t
K*(t)/ Y*(t)=const
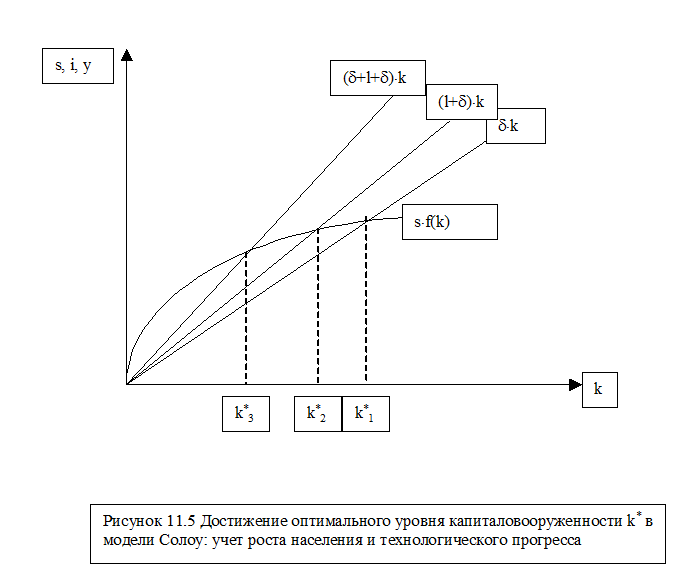 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.