Основные экономические школы и место новой классической экономики и школы реального делового цикла в общей структуре экономической теории, страница 45

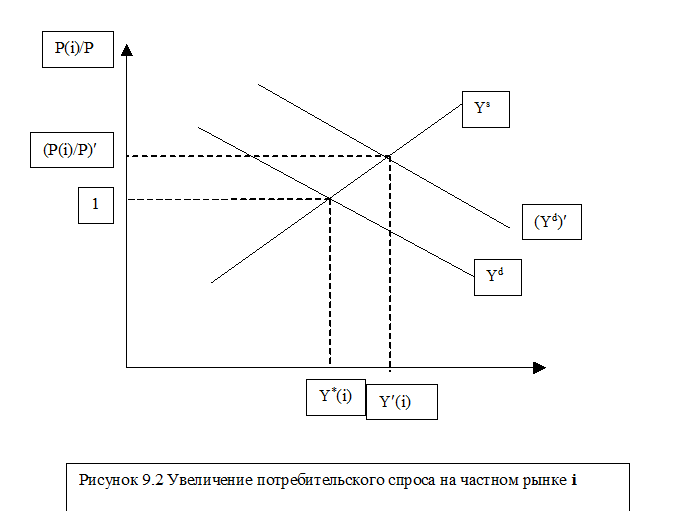
Предположим, что на рассматриваемом локальном рынке появляется дополнительный спрос на потребительские блага (на Рис 9.2 - сдвиг линии спроса вправо-вверх). Первое последствие этого события  - возрастание относительной цены на данном рынке. Это вызывает рост предложения товаров на данном рынке (сдвиг вдоль линии Y^s_t(i)), а также инвестиций и инвестиционного спроса.

Другой сюжет - увеличение денежной массы. Как мы знаем, свойство нейтральности денег состоит в том, что в ответ на увеличение денежной массы все цены растут одновременно, в данном случае - одинаково на всех локальных рынках и в той же пропорции, что и средний уровень цен на всех рынках. А это значит, что соотношение между ценами не меняется и относительная цена на данном рынке также не меняется. На графике не произойдет никаких сдвигов, и никакие реальные переменные не изменятся.

9.2 Модель равновесия локального рынка в условиях неполной информации и независимые результаты систематической монетарной политики

Теперь сделаем весьма близкое к реальности предположение о том, что агенты оперируют в условиях неполной информации: знают изменения цен лишь на продукцию, которую сами изготовляют и продают; относительно других цен, а, следовательно, и относительно среднего уровня цен экономические агенты формируют свои ожидания - строят прогнозы. Главная идея: люди знают больше о тех ценах, с которыми имеют дело, но могут только догадываться об остальных.

Будем также считать, что ожидания экономических агентов рациональны. Теория рациональных ожиданий утверждает, что для того, чтобы сформировать свои ожидания люди используют всю доступную им информацию, причем наилучшим образом (см. также лекцию 2). Кроме того, считаем, что все агенты имеют одинаковую доступную информацию, что приводит их к одной и той же ожидаемой средней цене - величине P^e_t. При этом в условиях рациональных ожиданий ошибка прогноза, равная (P_t- P^e_t), не имеет систематической составляющей, а является случайной переменной, такой, что ее математическое ожидание E((P_t- P^e_t)=0. Другим словами, экономические агенты в среднем правильно предсказывают изменение среднего уровня цен, хотя в отдельном частном случае могут ошибиться.

Для учета данного положения в построенной модели нужно вместо переменной среднего уровня цен P_t подставить переменную P^e_t, а вместо переменной P_t(i)/P_t, соответственно, P_t(i)/P^e_t. Последнюю относительную переменную назовем "ощущаемой ценой", т.е. такой, какой ее воспринимают экономические агенты.

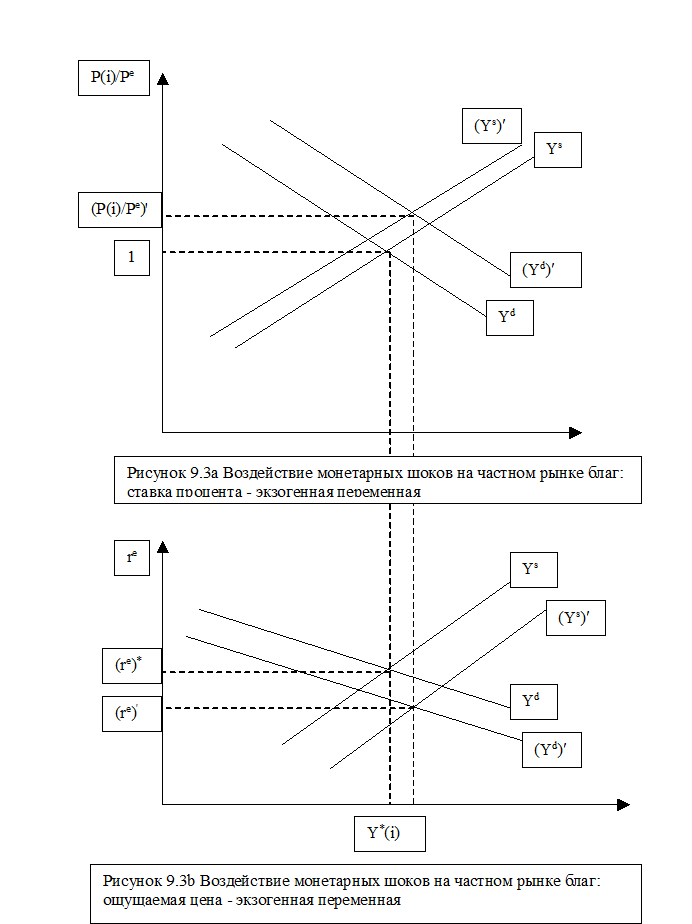
Построим график равновесия на частном рынке i в двух системах координат - (P_t(i)/P^e_t, Y(i))и (r^e, Y(i)) (Рис. 9.3). Чтобы построить график в первой системе координат (Рис. 9.3a) необходимо переменную r^eвыбрать на равновесном уровне, а для графика во второй системе координат требуется задать на равновесном уровне переменную ощущаемой цены, т.е. P_t(i)/P^e_t=1 (см. Рис. 9.3b).

Теперь, пусть произошел рост денежной массы, который привел к увеличению P_t(i). Возможны два исхода в зависимости от того, как меняется переменная P^e_t. Если экономические агенты не ожидают, что за ростом цены P_t(i) стоит увеличение денежной массы, то P^e_t не изменяется, а, следовательно, ощущаемая цена P_t(i)/P^e_t возрастает. В этом случае линию спроса на втором графике требуется сдвинуть влево-вниз, а линию предложения - вправо-вниз, таким образом, что доход возрастает, а норма процента снижается. Снижение нормы процента, в свою очередь приводит к сдвигам в системе координат (P_t(i)/P^e_t, Y(i)). Так, линия спроса должна быть сдвинута вправо-вверх, а линия предложения - влево-вверх. Результат - повышение цены на данном рынке, т.е. P_t(i)/P^e_t>1 и рост дохода. Отметим, что результат аналогичен последствиям, к которым приводит монетарная экспансия в модели IS-LM с жесткими ценами. Разница лишь в объяснении причин: в анализируемой модели цены не являются жесткими, тем не менее, монетарный шок воздействует на переменные реальной экономики. Причина - неполнота информации в условиях рациональных ожиданий.