ДОКАЗАТЕЛЬСТВО: см. Приложение к данной лекции.
Интересен вывод: рост потребления будет происходить одновременно во всех рассматриваемых периодах в независимости от того за счет роста дохода каких периодов происходит расширение бюджетных возможностей. Т.е. рост дохода только в первый период приведет к увеличению потребления и в первый период, и во второй. Точно также рост дохода во второй период сказывается на увеличении потребления уже и в первый период времени.
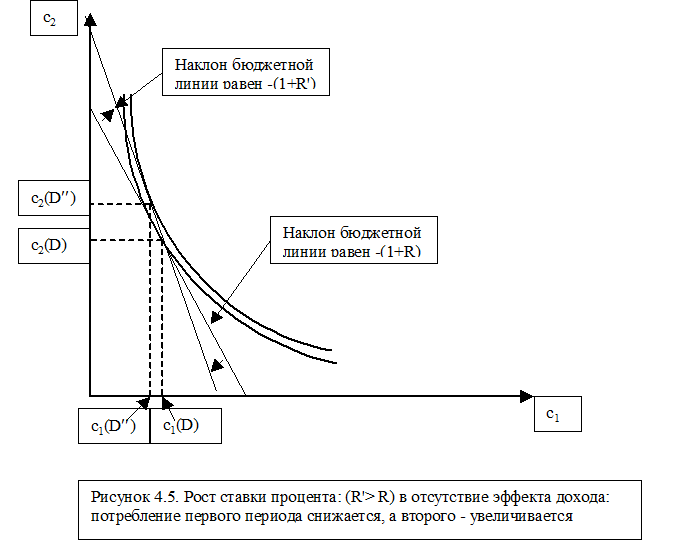
Теперь проведем анализ воздействия на потребления изменения ставки процента. Предположим, что она увеличивается до уровня R¢, что обуславливает и изменение величины бюджета до уровня D¢¢. В какую именно сторону меняется данная величина зависит от более или менее конкретных обстоятельств, поскольку рост ставки процента увеличивает одну составляющую суммы бюджета, но уменьшает другие. Мы выберем такую ситуацию, при которой набор [c1(D), c2(D)], оптимальный в задаче (4.2), (4.3), может быть куплен при бюджете D¢¢ и при этом весь бюджет D¢¢ расходуется полностью[12]. Это означает, что на соответствующем графике (см. Рис. 4.5) новая бюджетная линия пройдет в точности через точку [c1(D), c2(D)]. Кроме того, она пройдет круче первоначальной бюджетной линии, поскольку модуль величины ее наклона возрастает. Сформулируем следующее утверждение:
УТВЕРЖДЕНИЕ 2. Пусть даны задача (4.2), (4.3), в которой функция полезности обладает свойствами (4.1) и ее решение [c1(D), c2(D)]. Пусть ставка процента возрастает с уровня R до уровня R¢, таким образом, что
c1(D)+ c2(D)/(1+R¢)=D¢¢,
где D¢¢ - сумма бюджета после увеличения ставки процента. Тогда имеют место следующие соотношения:
c1(D)> c1(D¢¢)
c2(D)< c2(D¢¢)
где [c1(D¢¢), c2(D¢¢)]есть решение задачи (4.1), (4.2) при ставке процента R¢.
ДОКАЗАТЕЛЬСТВО: см. Приложение к данной лекции.
Соответствующий эффект - изменение объемов потребления в ответ на изменение ставки процента - принято называть эффектом межвременного замещения от изменения процента. Однако он затрагивает не только потребление. Из предыдущей лекции нам известно, что свободное время - также есть благо, причем нормальное благо. Это, в частности, значит, что рост ставки процента приведет к перераспределению свободного времени в пользу будущего периода, т.е. к увеличению трудовых усилий в текущем периоде, вызывающий, в свою очередь, рост производства в указанный период. Рост производства при снижении потребления означает также и рост нормы сбережения, определяемой как отношение сберегаемой части дохода ко всему доходу рассматриваемого периода времени. Понятно, что снижение ставки процента ведет к противоположным последствиям для текущего периода: к росту потребления, снижению занятости и нормы сбережения.
 |
4.4 Многопериодная оптимизация: теория жизненного цикла и теория постоянного дохода
4.4.1 Теория жизненного цикла и неизменный уровень потребления
Теперь введем в рассмотрение большее количество периодов времени. Базируясь на теории жизненного цикла Франко Модильяни, следует принять за основу горизонт жизненного цикла, N- количество лет, которое рассматриваемый индивидуум ожидает прожить. Выделяется также рабочий период W - число лет до выхода на пенсию, который меньше периода жизни: W<N, разница между ними составляет период, когда индивидуум живет за счет сбережений, накопленных за время работы. Считается также, что наследства он не оставляет, т.е. его потребление за весь жизненный цикл в точности равно его первоначальному богатству плюс его заработок за время рабочего периода.
Строго говоря, ставка процента в рассматриваемом ниже уравнении может меняться от года к году. Однако мы рассмотрим ее неизменной, считая, что индивидуум находится в первом году, все последующие годы относятся к ожидаемому периоду времени, а ставка процента R - ожидаемая средняя величина. Итак, бюджетное ограничение для периода жизненного цикла имеет следующий вид:
b0/P×(1+R)+y1+y2/(1+R)+y3/(1+R)2+…+yW/(1+R)W-1=
=c1+c2/(1+R)+c3/(1+R)2+…+cN/(1+R)N-1
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.