Основные экономические школы и место новой классической экономики и школы реального делового цикла в общей структуре экономической теории, страница 22

Рассмотрим предпочтения представительного агента.Для этого зададим функцию полезности u(c₁, c₂), определенную на множестве потребительских наборов для двух периодов (c₁,c₂) с обычными свойствами:

¶u/¶c_i>0, ¶²u/(¶c_i)²£0, ¶u²/(¶c_i׶c_j)>0                                       (4.1)

Множество предпочтений задается кривыми безразличия (см. Рис. 4.2). Для данного уровня полезности u₀ можно записать:

dc₂/dc₁|_u=u0=-¶u/¶c₁:¶u/¶c₂

где -¶u/¶c₁:¶u/¶c₂есть наклон данной кривой безразличия в соответствующей точке.

4.2.3 Равновесие потребителя

Совмещение бюджетного ограничения и множества кривых безразличия приводит к задаче оптимизации потребителя для двух периодов, известной также как модель Фишера:

max{u(c₁,c₂)}                                                                      (4.2)

c₁+c₂/(1+R)=D                                                                     (4.3)

Выразим с₂ через с₁ и сформируем новую функцию полезности:

U(c₁)=u(c₁, [D×(1+R)-c₁×(1+R])

Взяв ее производную по c₁ и поделив все на ¶u/¶c₂, получим:

(dU/dc₁)/(¶u/¶c₂)=(¶u/¶c₁)/(¶u/¶c₂)-(1+R)

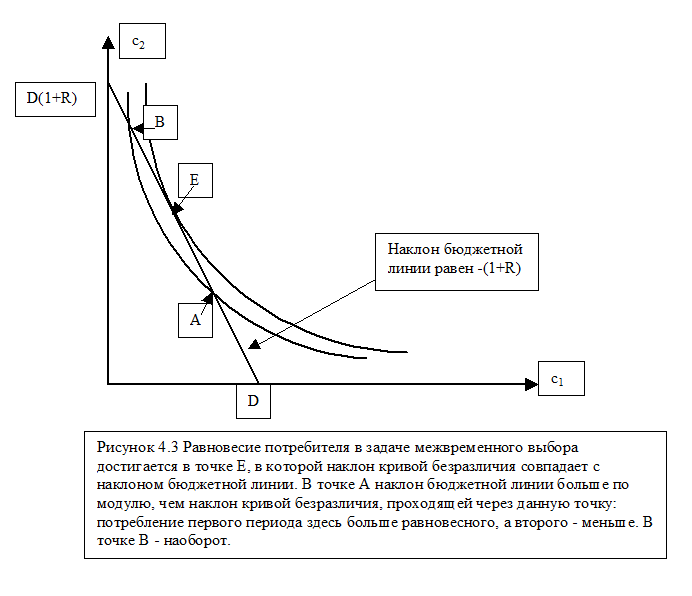
Функция U(×)имеет положительный знак, если рост c₁ приводит к росту функции u(×) и отрицательный, если - к снижению. Оптимальное состояние рассматриваемого домохозяйства (или, что то же - равновесие домохозяйства) достигается тогда, когда U(×)=0. На Рис. 4.3. видно, что если в какой-либо точке модуль наклона кривой безразличия (¶u/¶c₁)/(¶u/¶c₂)больше, чем модуль наклона бюджетной линии 1+R то потребление первого периода следует увеличить и наоборот. Оптимальное решение [c₁(D), c₂(D)]имеет место тогда, когда наклон кривой безразличия в общей с бюджетной линией точке совпадает с наклоном бюджетной линии:

(¶u/¶c₁)/(¶u/¶c₂)=1+R

В этом случае предельная норма замещения потребления первого периода потреблением второго периода в точности равна альтернативным издержкам потребления в первый период, выраженным в единицах потребления второго периода.

Указанные результаты оформим в виде следующей леммы:

ЛЕММА 1: Пусть дана задача (4.2), (4.3), в которой функция полезности обладает свойствами (4.1) и ее решение [c₁(D), c₂(D)]. Для каждой точки (c₁, c₂) лежащей на бюджетной линии верны следующие утверждения:

Если (¶u/¶c₁)/(¶u/¶c₂)>1+R,то c₁< c₁(D) и c₂> c₂(D)

Если (¶u/¶c₁)/(¶u/¶c₂)<1+R,то c₁> c₁(D) и c₂< c₂(D)

Если (¶u/¶c₁)/(¶u/¶c₂)=1+R, то c₁= c₁(D)и c₂=c₂(D)

ДОКАЗАТЕЛЬСТВО: очевидно.

4.3 Воздействие шоков предложения: эффект дохода и эффект межвременного замещения

Теперь предположим, что происходит позитивный шок предложения. Мы знаем, что такой шок приводит к росту потребления в тот же период времени все равно, является ли он параллельным или пропорциональном, однако, во втором случае результат носит более выраженный характер. Другое различие состоит в изменении интенсивности труда: при параллельном шоке она снижается, а при пропорциональном - результат не определен. Поскольку в рассматриваемой модели Фишера трудовые усилия не рассматриваются, то указанный аспект здесь не так важен; важен лишь рост потребления при позитивном шоке и его снижение при негативном.

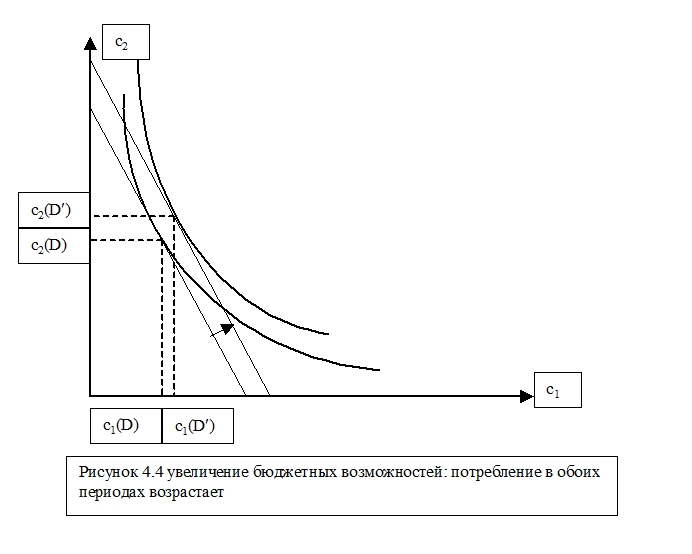Рассмотрим эффект дохода, возникающий при увеличении бюджетных возможностей Dдо уровня D¢, что имеет место тогда, когда производственная функция становится более продуктивной. Не трудно видеть, что на графике это отражается параллельным сдвигом бюджетной линии в направлении от начала координат, поскольку ее наклон зависит лишь от нормы процента, которая не меняется. Новая задача имеет тот же вид, что и раньше (за исключением одного параметра - D¢вместо D). Ее решение [c₁(D¢), c₂(D¢)] показано на Рис. 4.4. Для нас важно, что оба рассматриваемых блага являются нормальными, т. е. при увеличении суммы бюджета их потребление возрастает. Сформулируем это в виде утверждения 1:

УТВЕРЖДЕНИЕ 1. Пусть дана задача (4.2)-(4.3), в которой функция полезности обладает свойствами (4.1). Тогда объемы потребления в обоих периодах являются нормальными благами.