Основные экономические школы и место новой классической экономики и школы реального делового цикла в общей структуре экономической теории, страница 44

Для определения того, сколько производить, используется уже предельный продукт труда не физический, а реальный - P_t(i)/P_t×MPL_t. Таким образом, рост относительной цены приводит к последствиям, аналогичным пропорциональному шоку предложения, а, следовательно, росту физического предельного продукта труда. Как мы знаем, при этом имеют место три эффекта - эффект дохода, приводящий к снижению трудовых усилий, эффект замещения, который, наоборот, способствует росту трудовых усилий и эффект межвременного замещения, вызываемый ростом дохода. Последний эффект связан с тем обстоятельством, что рост относительной цены не может восприниматься агентами как постоянное изменение, поскольку агенты осведомлены, что отклонения цен на данном рынке от среднего уровня носят, скорее, временный характер. По этой же причине эффект дохода будет достаточно слабым, чтобы его не принимать во внимание. Это означает, что в результате увеличения цены произойдет рост трудовых усилий, а, значит, и рост предложения продукции на данном рынке.

Теперь рассмотрим как на рост относительной цены реагируют инвестиции в данном регионе, а следовательно и инвестиционный спрос. Мы по-прежнему предполагаем, что между инвестициями и производством продукции существует временной лаг, равный одному временному периоду. Далее, будем считать, что инвестиционные товары покупаются по общей цене P_t (поскольку они могут приобретаться на любых рынках), а через один период времени данные единицы капитала стоят также общей цены P_t+1. Продажа продукции осуществляется по цене локального рынка P_t+1(i). Отвлечемся от возмещения капитала и определим предельную норму норма возврата капитальных вложений, которая должна быть равна ожидаемой номинальной ставке процента R^e:

[P_t+1(i)×MPK_t(i) + P_t+1]/P_t  -1 = R^e

Обозначим через p_t уровень инфляции. Тогда имеем следующее соотношение:

(1+p_t)×[P_t+1(i)/P_t+1×MPK_t(i)+1]=(1+p_t)*(1+r^e)

или:

P_t+1(i)/P_t+1×MPK_t(i)=r^e.

Это означает, что, когда цена P_t+1 растет относительно среднего уровня, то и спрос на инвестиции агентов, функционирующих на данном рынке, возрастает ввиду увеличении объема их желаемого капитала. Тогда можно утверждать, что возрастает и спрос на инвестиционные товары со стороны агентов экономики в данном регионе.

Спрос на потребительские блага c^d_t(i) будет снижаться, если величина P_t(i)/P_t возрастает. Это можно утверждать по той причине, что закупки потребительских благ сокращаются, когда их цена возрастает.

9.1.3 Модель равновесие на локальном рынке

Итак, теперь можно записать модель для рынка i:

Y^s_t(i)(P_t(i)/P_t, r^e,..) = C^d_t(i)(P_t(i)/P_t,r^e_t,..)+I^d_t(P_t+1(i)/P_t+1, r^e…)

(+)    (+)                       (-)   (-)                  (+)       (-)

Если P_t(i)/P_t меняется определенным образом, например, возрастает, то экономическим агентам будет рационально предположить, что такое соотношение между ценой на данном рынке и средним уровнем цен сохранится и на следующий период времени. Другими словами, экономические агенты, видя, что относительная цена на данном рынке возрастает в период t, ожидают, что и на следующий период t+1цена останется на более высоком уровне. Поэтому можно упростить полученное соотношение, заменив переменную P_t+1(i)/P_t+1 на переменную P_t(i)/P_t:

Y^s_t(i)(P_t(i)/P_t, r^e,..) = C^d_t(i)(P_t(i)/P_t,r^e_t,..)+I^d_t(P_t(i)/P_t, r^e..),

(+)    (+)                       (-)   (-)            (+)       (-)

а затем еще и записать более коротко:

Y^s_t(i)(P_t(i)/P_t,r_t,..) = Y^d_t(i)(P_t(i)/P_t,r^e_t,..)

           (+)   (+)                         (-)   (-)

где

Y^d_t(i)(P_t(i)/P_t,r^e_t,..)= C^d_t(i)(P_t(i)/P_t,r^e_t,..)+I^d_t(P_t(i)/P_t,r^e..).

(-)   (-)                   (-)      (-)            (+)      (-)

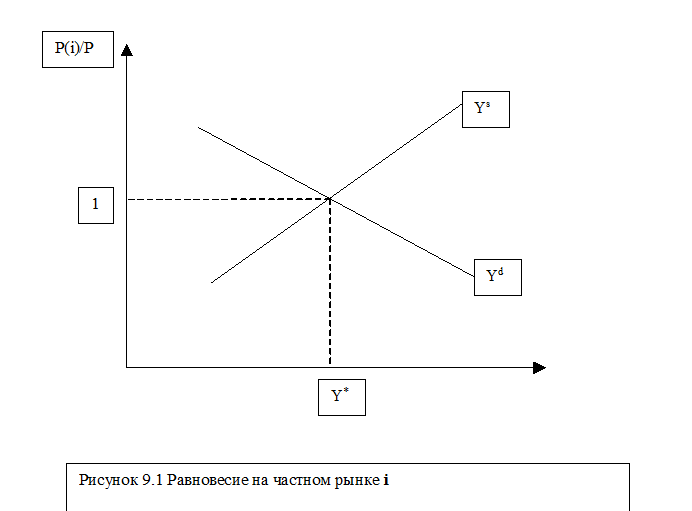
Спрос на потребительские товары и инвестиционный спрос по-разному ведут себя при изменении относительной цены P_t(i)/P_t - потребительский спрос падает с ее ростом, а инвестиционный - наоборот. Первый эффект, однако же, сильнее: доля потребления в доходе выше, чем инвестиций. Следовательно, общий спрос Y^d_t(i) уменьшается с ростом P_t(i)/P_t, что мы и зафиксировали подстрочным знаком (-). На графике (Рис. 9.1) представлено равновесие на типичном рынке i. Оно устанавливается тогда когда P_t(i) = P_t, а следовательно P_t(i)/P_t = 1.