Основные экономические школы и место новой классической экономики и школы реального делового цикла в общей структуре экономической теории, страница 34

Рассмотрим общую модель уравновешивания рынков, считая, что агенты экономики ожидают равномерного роста денежной массы тем темпом, который они наблюдают в текущий период. В этом случае условия уравновешивания рынков благ и денег принимают вид:

Y^s(r,...)=C^d(r,...)

   (+)           (-)

M^s_t=P_t×Ф(R_t, Y,...)

(-) (+)

Пусть имеет место рост номинальной денежной массы темпом прироста m. Тогда можно записать, что

M^s_t =M_t =M_t-1×(1+m),

где M_t есть обозначение для объема денежной массы в экономике. Согласно полученным в предыдущих разделах выводам, ежегодный рост денежной массы не повлечет за собой никаких изменений спроса или предложения на рынке товаров, что есть проявление свойства нейтральности денег. С другой стороны, как мы знаем, рост денежного предложения вызывает пропорциональный рост цен. Постоянный темп роста денежного предложения означает такой же постоянный темп роста цен. При этом, согласно уравнению Фишера, номинальная ставка процента есть реальная ставка процента "плюс" темп прироста цен, т.е.

R=r+p.

Результатом является тот факт, что на рынке денежных активов реальное денежное предложение является неизменным и равным реальному же денежному спросу.

Следовательно, при постоянном росте денежной массы в условиях равновесия на рынках благ и денег (а, следовательно, и на рынке активов приносящих доход) будут выполняться следующие условия:

1) темп прироста цен равен темпу прироста денежной массы: p=m[16]

2) реальная денежная масса остается неизменной: M/P=const

3) номинальная ставка процента остается неизменной, в силу неизменности реальной ставки процента и уровня инфляции: R=r+p=const.

7.4.2 Изменение темпов инфляции: проблемы нейтральности и супернейтральности денег

Теперь поставим вопрос следующим образом: что произойдет с основными макроэкономическими показателями при увеличении темпа роста номинального денежного предложения? Для того, чтобы дать ответ на указанный вопрос удобнее будет перейти от дискретной динамической модели к непрерывной, т.е. рассматривать все переменные как непрерывные функции от времени. Запишем ее, приняв во внимание, что R=r+p.

Y^s(r(t),...)=C^d(r(t),...),

     (+)              (-)

M(t)=P(t)×Ф([r(t)+p(t)], Y(t),...),

                            (-)           (+)

M(t)=M₀×e^m×t,

p(t)=[dP(t)/dt]:[P(t)]

Данная модель включает темп прироста денежной массы m как экзогенную переменную и позволяет определить равновесные значения Y^*, C^*, r^*, P^*, p^*, R^*. При данном m равновесная динамика будет характеризоваться следующими условиями:

Y(t) =C(t)=Y^*=C^*=const,

p(t)=p^*=const,

R(t)=R^*=r^*+p^*=const,

M(t)=M₀×e^m×t,

P(t)=P₀×e^p(t)×t=P₀×e^m×t

Прологарифмируем два последних уравнения:

ln(M) = ln(M₀) + m×t и

ln(P)=ln(P₀)+p^*×t.

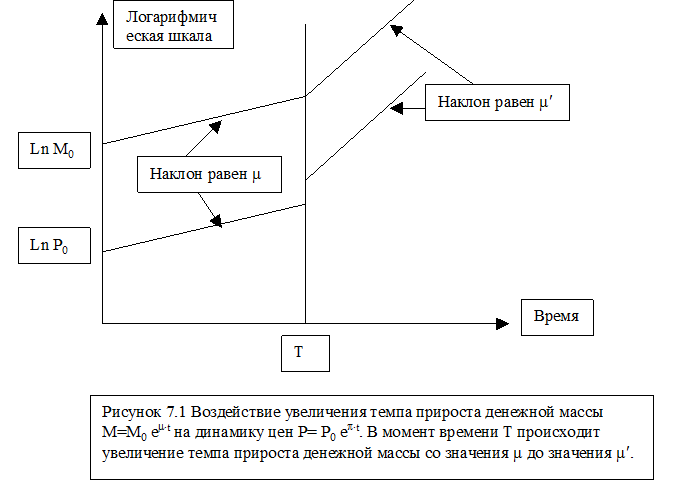
Графики этих функций в логарифмической шкале являются линейными с наклоном равным m, поскольку p(t)=p^*=m (см. Рис 7.1).

Пусть в момент T происходит увеличениеm до уровня m¢. Будем сначала считать, что имеют место совершенные ожидания относительно скорости роста денежной массы и цены могут меняться мгновенно. Тогда  в сформулированной выше модели следует последнее уравнение

p(t)=[dP(t)/dt]:[P(t)]

заменить на

p(t)=m

В этом случае, как видно на графике, в момент T, во-первых, наклон обоих графиков возрастает с величины mдо величины m¢. Во-вторых, уровень цен получает дополнительный импульс роста, что приводит к снижению объема реальной денежной массы в экономике M/P. Это происходит потому, что одновременно, в момент T, происходит рост номинальной ставки процента с величины r+m до величины r+m¢, что снижает спрос на реальные денежные активы Ф(×).

Каков механизм данного события? Если агенты экономики осведомлены, что центральный банк должен провести указанную акцию, то ожидается, что в момент T темп роста цен вырастет в связи с ростом темпа денежной массы. Заемщики средств начнут увеличивать спрос на денежные активы, а кредиторы - сокращать (или, наоборот, в терминах облигаций: предложение облигаций будет расти, а спрос на них - сокращаться), поскольку при прежней номинальной норме процента ожидаемая реальная норма снижается: r^e(T) = R-p^e(T). Следовательно, R начинает расти и растет до тех пор, пока новый уровень номинального процента не будет равен r^*+m'. В этом случае инфляция вновь стабилизируется, но на новом уровне p(t)=m'. Обращаем внимание, что при этом, при прежних значениях дохода Y^*, потребления C^*, реальной ставки процента r^*, спрос на реальные денежные активы снижается: