Основные экономические школы и место новой классической экономики и школы реального делового цикла в общей структуре экономической теории, страница 56

11.1 Множество производственных возможностей и свойства производственной функции

Обозначения, которые мы используем в данном контексте, несколько отличаются от тех, которыми мы пользовались раньше. Именно, макроэкономическая производственная функция является функцией труда и капитала, но последний фактор, как уже говорилось, входит в нее без временного лага:

Y = F(K, L)

(+)(+)

где K - объем физического капитала, L - численность занятых в экономике. Данная функция описывает эффективные варианты множества производственных возможностей и характеризуется постоянной отдачей от расширения масштаба, что означает, что увеличение применения всех производственных ресурсов в одинаковое количество раз, скажем в r раз, приводит к росту выпуска также в r раз:

r×Y = F(r×K, r×L)

При этом, как не трудно видеть, сумма коэффициентов эластичности выпуска по обоим факторам производства равна 1:

e_K+e_L = (¶Y/¶K)×(K/Y)+(¶Y/¶L)×(L/Y) = 1

Насколько верно такое представление? Оно скорее верно для государств с невысокой плотностью размещения хозяйства по территории. Дело в том, что важным производственным фактором является земля (более широко - природные ресурсы). Если земли достаточно, то она не ограничивает производство, если - земельных ресурсов мало, то производство наталкивается на их нехватку и производственная функция от капитала и труда становится функцией с убывающей отдачей от масштаба. Как показывают эмпирические исследования, для большинства стран мира описание производственных возможностей при помощи производственной функции с постоянной отдачей от расширения масштаба вполне приемлемо.

Нам будет удобно сначала обсудить динамику экономики при данной технологии и данной численности населения. Последнее означает также и то, что уровень занятых в экономике не меняется, поскольку, как отмечалось выше, мы исходим из заданного уровня занятости.

При данном уровне занятости можно нарисовать график производственной функции, имеющий вогнутый характер (Рис. 11.1). Наклон линии производственной функции измеряется предельной производительностью капитала. Рост эффективности производства, связанный, как мы знаем, с позитивным шоком предложения, приводит к смещению графика вверх, что, как правило, увеличивает и предельную производительность капитала. Большему значению K соответствует большее значение выпуска Y.

11.2 Тождество национальных счетов и уравнение воспроизводства капитала

Рассмотрим тождество национальных счетов в закрытой экономике. Его можно записать в виде: S=I, где S - национальное сбережение, а I - валовые инвестиции в основной капитал. Далее, сбережения запишем по-другому - задав норму сбережения в доходе s, а инвестиции разобьем на чистые инвестиции dK/dt и инвестиции на возмещение выбывающего основного капитала d×K, где d - норма выбытия капитала. В результате получим следующее уравнение:

s×Y = dK/dt +d×K,

или

dK/dt = s×F(K,L) - d×K.

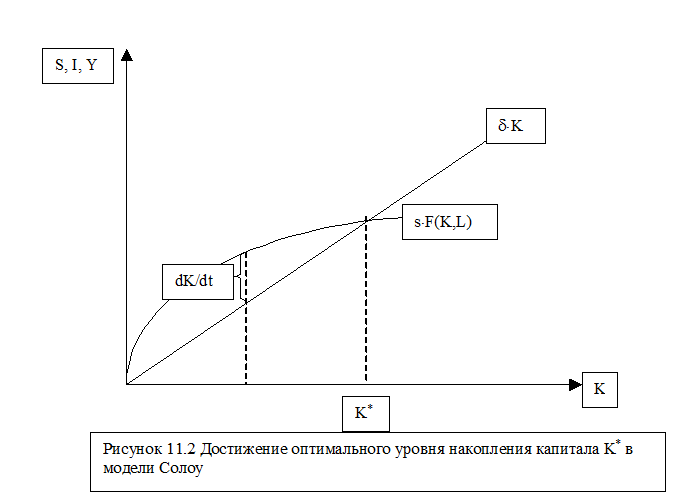На графике (Рис. 11.2) представим линию сбережений s×F(K,L), которая получается пропорциональным сдвигом графика производственной функции вниз и имеет вогнутый характер, и отдельно - линейный график возмещения капитала d×K. В точке их пересечения при уровне капитала K^* чистые инвестиции равны нулю; это значит, что в данной точке достигается максимально возможный объем капитала, а, следовательно, и выпуска. Одновременно, поскольку доля дохода, идущая на инвестиции фиксирована, то максимально возможным оказывается и объем потребления, а поскольку численность населения также рассматривается пока как неизменная, то и душевой объем потребления также достигает максимума. Соответствующее состояние экономической системы назовем стационарным. При таком состоянии имеют место нулевые темпы роста труда (по предположению), капитала dK/dt=0, а, значит и выпуска: dY/dt. Кроме того, такое состояние является устойчивым, поскольку оно воспроизводится во времени. Последнее означает, что отклонение от оптимального объема капитала устраняется силами саморегулирования самой экономической системы. Например, если K>K^*, то объем выбытия капитала начинает превышать объем сбережений и инвестиций, а, следовательно, чистые инвестиции становятся отрицательными: dK/dt<0, следовательно, объем капитала уменьшается вплоть до достижения уровня K^*. Если же K<K^*, то чистые инвестиции больше нуля и объем капитала растет пока не достигнет уровня K^*[21]