Основные экономические школы и место новой классической экономики и школы реального делового цикла в общей структуре экономической теории, страница 14

Указанные условия означают, что каждое дополнительное трудовое усилие приносит полезный результат - дополнительный продукт, но меньший, чем предыдущее. Второе условие, носит, как известно, название закона убывающей производительности, характерного для процессов производства в краткосрочной перспективе, когда нельзя изменить количество всех применяемых факторов. Таким образом, подспудно считается, что труд, переменный производственный фактор, не есть единственный производственный фактор, а фактически имеются и другие или другой, которые являются постоянными. Это может быть, например, участок земли, используемый натуральным хозяйством, возможность расширения которого не рассматривается. График производственной функции (Рис. 3.1), таким образом, имеет вогнутый вид: наклон его уменьшается с ростом l, как это показано на Рис. 3.1 - наклон касательной в точке A, больше наклона касательной в точке B, при том, что l^A<l^B. Рассмотрим также предельный продукт труда как функцию от его затрат MP_L(l)=dy/dl(l). Закон убывающей производительности означает, что это убывающая функция, следовательно, ее график (см. Рис. 3.2) имеет отрицательный наклон.

Производственная функция является обобщающей характеристикой условий производства и зависит от многих факторов, таких как уровень применяемых технологий, доступность общественных благ, природных факторов. Так, если рассматривается фермерское хозяйство, то природно-климатические условия могут приобретать особую важность и их изменение приводит к изменению самой производственной функции, что на графике может быть показано его сдвигами (Рис. 3.3). Указанные сдвиги также могут соответствовать изменениям умелости фермера при тех же средствах труда. За ними могут стоять и изменения самой технологии, используемой рассматриваемым агентом экономики. Во всех случаях речь идет о шоках предложения[6]. Шок предложения - есть внешнее изменение условий производства. Естественно выделить негативные шоки, связанные с ухудшением условий производства, и позитивные, за которыми стоит увеличение производительности применяемых факторов (на Рис. 3.3 - линия f¹(l) сдвигается до положения f²(l)).

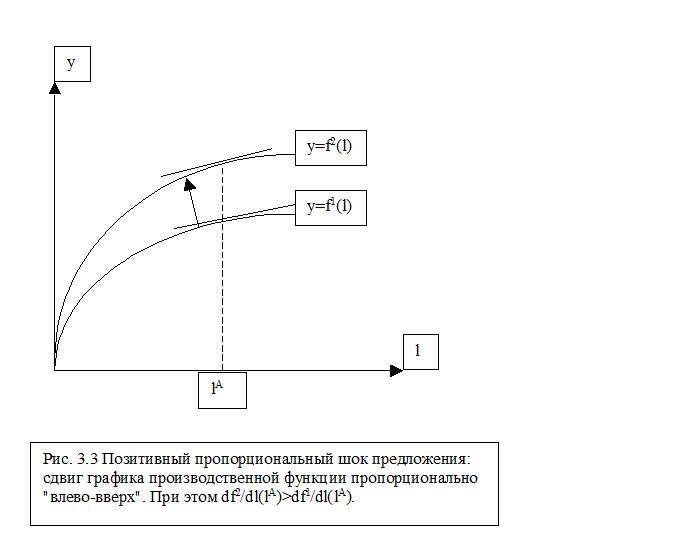Изображенный на Рис. 3.3 сдвиг производственной функции называется пропорциональным сдвигом, т.е. таким, что одновременно с перемещением графика вверх (или вниз при негативном шоке) в том же направлении меняется и его наклон - увеличивается или уменьшается. Алгебраически пропорциональный сдвиг может быть достигнут простым умножением производственной функции на постоянную величину[7]. Очевидно, что в каждой точке графика значения вновь полученной функции будут при этом одинаково соотноситься со значениями исходной производственной функции, и, таким образом, средняя производительность производственного фактора изменится одинаково в каждой точке:

AP_L²(l) : AP_L¹(l)= k×f(l)/l : f(l)/l = k,

где AP_L²(l) - функция средней производительности после сдвига, AP_L¹(l) - исходная функция средней производительности, k - константа сдвига. Другое свойство пропорционального сдвига производственной функции в изменении графика предельной производительности. При умножении производственной функции на константу k график функции предельной производительности также сдвигается пропорционально с константой сдвига, равной k:

MP_L²(l) : MP_L¹(l) = k×dy/dl : dy/dl = k.

Таким образом, график функции предельной производительности смещается аналогично графику производственной функции: вверх - при позитивном шоке, и вниз - при негативном.

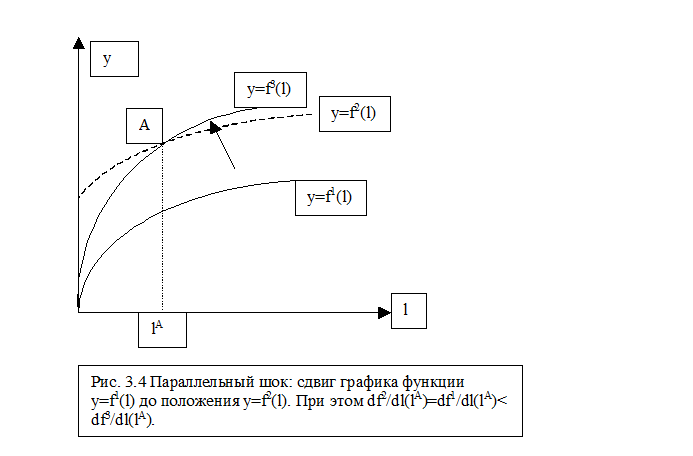Пропорциональный сдвиг производственной функции можно разделить на две составляющие: параллельный сдвиг, учитывающий только изменение средней производительности фактора производства, и изменение наклона границы производственных возможностей вокруг какой-либо точки на линии графика (на Рис. 3.4- вокруг точки A). Параллельный сдвиг можно рассматривать и как особый тип сдвига производственной функции. Он достигается не умножением производственной функции на некоторую постоянную величину, а ее прибавлением к ней. В этом случае меняется средняя производительность: