d=g/((1+g)j+1-1)
Ясно, что величину выбытия капитала можно считать постоянной, поскольку она зависит от g- среднего темпа прироста инвестиций за достаточно длительный период, который не может меняться слишком быстро.
Таким образом, можно считать, что выбытие капитала в году t есть dt=d×kt-1. Тогда в конце периода t объем капитала составит:
kt=kt-1+it -d×kt-1.
Величина it - валовые инвестиции - все закупки капитальных благ в течение данного периода. В отличие от валовых инвестиций есть еще понятие чистых инвестиций:
kt-kt-1 = it-d×kt-1.
Соответственно есть две концепции выпуска или продукта: валовой выпуск yt - весь предлагаемый товар на рынке, и чистый выпуск (продукт) yt-d×kt-1. Он имеет смысл всех тех благ, которые могут быть использованы для потребления или расширения основного капитала.
Для построения модели введем некоторые допущения относительно используемого физического капитала.
- сделанные инвестиции не могут быть использованы в качестве потребительских благ, что составляет свойство необратимости инвестиций. Однако имеется возможность не возмещать выбывающий капитал,
- капитал является идентичным во всех областях применения, следовательно, необходимо допустить, что предельный продукт капитала каждого агента одинаков. За этим стоит также то допущение, что капитал размещен наилучшим образом,
- допускается возможность перепродажи капитала: если для данного агента предельный продукт капитала слишком низок, то он может продать какую-то его часть на рынке капитальных благ по той же цене, что и новый капитал.
8.3 Желаемый капитал
Теперь опишем, как формируется спрос на инвестиции. Ясно, что решение о закупке дополнительной единицы капитала в период t-1 осуществляется на основе сопоставления издержек и выгод. Прямые издержки равны Pt-1, т.е. цене единицы капитального блага в годуt-1. Но имеются и выгоды, причем, двоякого рода:
- Pt×MPKt-1 выручка от дополнительной продукции,
- сам капитал в объеме Pt×(1-d), который может и дальше использоваться фирмой, или быть реализован на вторичном рынке инвестиционных товаров.
Таким образом, отдача на единицу дополнительно введенного капитала составит:
(Pt×MPKt-1+Pt×(1-d)-Pt-1)/Pt-1 = (1+pt)×(MPKt-1+1-d)-1
Теперь рассмотрим альтернативу для инвестиций – предоставление займов. Вложение будет выгодно для потенциального инвестора, если и до тех пор, пока отдача данного вложения остается не ниже номинальной нормы процента R. В силу убывающей отдачи от использования фактора капитала последняя единица инвестиций должна приносить такой же эффект, какой приносит покупка облигации, т.е.:
(1+pt)×(MPKt-1-d)-1=Rt,
или, после преобразования:
MPKt-1-d = rt,
что и определяет спрос на капитал, т. е. желаемый капитал. Кривая спроса на капитал изображается сдвигом графика предельного продукта на величину d(см. Рис. 8.2). При помощи данного графика при заданной реальной ставке процента теперь можно определить желаемый капитал k*t.
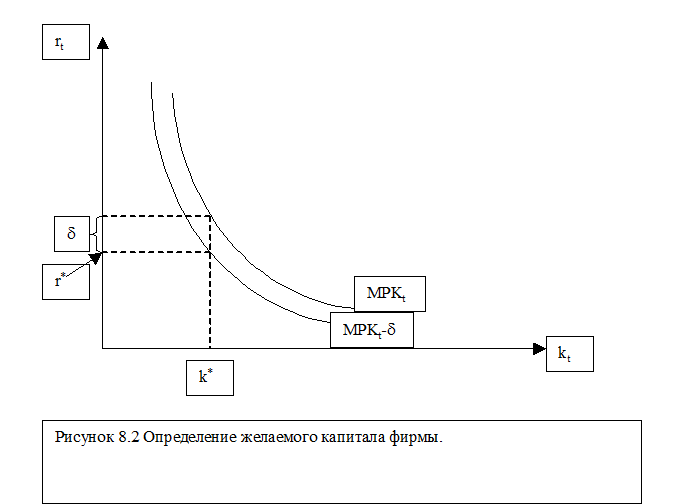 |
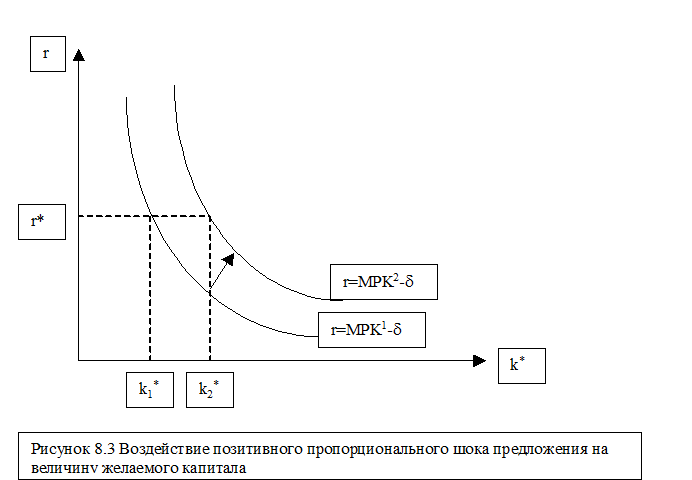
Нетрудно видеть, что чем эффективнее используемая технологии, тем выше желаемый капитал. В частности позитивный пропорциональный шок предложения приводит к сдвигу графика желаемого капитала вверх (см. Рис. 8.3), что при том же уровне реальной ставки процента ведет к росту желаемого капитала. Точно также можно видеть, что чем выше норма выбытия капитала, тем меньше желаемый капитал. Повышение реальной ставки процента, также уменьшает желаемый капитал. Функция спроса на капитал, таким образом, имеет следующий вид:
k*t = k*t(rt, d,...)
(-) (-)
8.4 Инвестиционная функция и спрос на капитал
Если предположить, что желаемый капитал может быть достигнут за один год, т.е. если отвлечься от инвестиционных лагов, то можно записать спрос на валовые инвестиции в следующем виде:
it= k*t - (1-d)×kt-1
или:
it= k*t(rt, d,...) - (1-d)×kt-1=it(rt, d, kt-1...)
(-) (?)(-)
Указанное выражение также носит название инвестиционной функции.
 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.