Основные экономические школы и место новой классической экономики и школы реального делового цикла в общей структуре экономической теории, страница 28

6.3.1 Уравновешивание рынка труда

Рассмотрим уравновешивание рынка труда. Основное уравнение равновесия выглядит следующим образом:

L^d(W/P,...) = L^s(W/P, R,...)                                                          (6.1)

                  (-)                  (+)   (+)

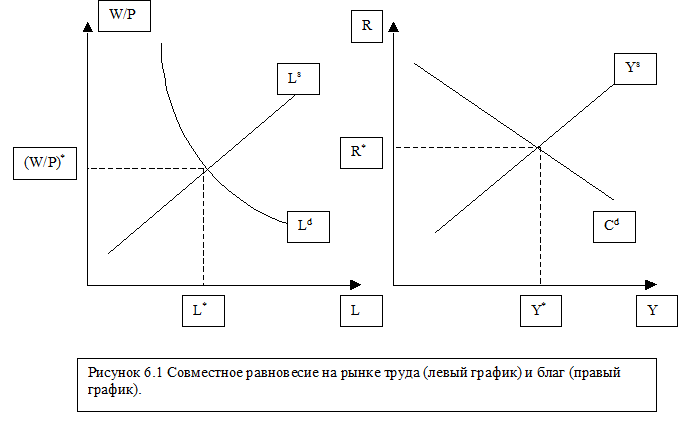
Вспомним, что ранее мы уже определяли параметр R и параметр P. Здесь мы имеем новое уравнение и новую переменную W/P, которая, по нашему предположению, меняется таким образом, чтобы уравновесить рынок труда. Функция L^d задана у нас, поскольку задана производственная функция, функция L^s задана, поскольку задано бюджетное ограничение домашних хозяйств и множество их предпочтений в потреблении (между потреблением и свободным временем). Теперь мы даем возможность меняться параметру W/P так чтобы сбалансировать спрос на труд со стороны фирм и предложение труда домашними хозяйствами. Результат балансирования - равновесная занятость L^* и равновесная реальная ставка заработной платы (W/P)^*. На графике (Рис. 6.1) представлено равновесие на рынке труда. Чтобы нарисовать в данной системе координат линию предложения труда, необходимо задаться определенным значением ставки процента R, которая может быть найдена исходя из условий равновесия на товарном рынке.

6.3.2 Уравновешивание рынка благ

Рассмотрим уравновешивание товарного рынка. Само уравнение равновесия отличается от того, что мы рассматривали в прошлой лекции, поскольку в данном случае используемые функции зависят от других переменных: кроме объясняющей переменной R , в них входит также эндогенная переменная  реальной ставки заработной платы W/P. Итак, для рынка товаров имеется уравнение:

СL^d(W/P, R,...) = YL^s(W/P)                                                                 (6.2)

(+)    (-)                  (-)

Модель для двух рынков включает уравнения (6.1) и (6.2) и две переменные - реальную ставку заработной платы и ставку процента. Решив указанную задачу можно найти равновесные значения (W/P)^*, R^*и Y^*.

6.3.3 Соотношение между ставками заработной платы и процента

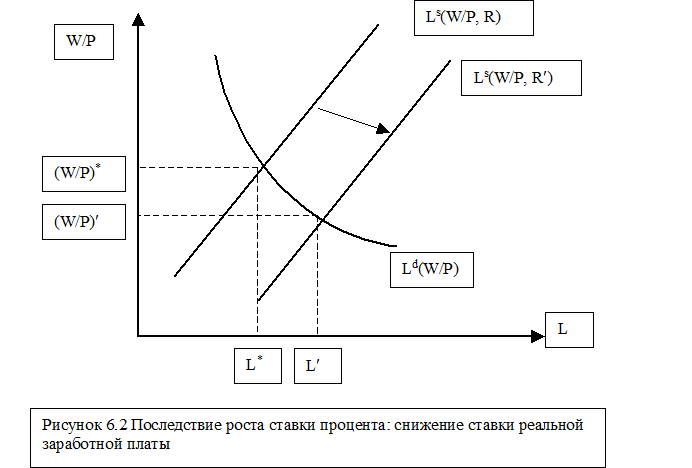
Строго говоря, переменные (W/P)^* и R^* не являются совершенно независимыми. Посмотрим, как повлияет на условия равновесия изменение ставки процента. Если R растет, то при той же самой реальной заработной плате предлагается больше труда. Следовательно на графике рынка труда , линия предложения труда сдвинется вправо (см. Рис. 6.2). Это в свою очередь приведет к снижению уровня реальной заработной платы. В самом деле: рост ставки процента означает увеличение трудовых усилий, а, следовательно, снижение предельного продукта труда. Это значит, что эффект изменения нормы процента на рынке труда можно описать следующим образом:

W/P= W/P(R), где d(W/P)/dR<0                                                                        (6.3).

6.3.4 Сравнение агрегированной модели уравновешивания и модели уравновешивания с выделением рынка труда

Если полученную функциональную зависимость (6.3) подставить, в уравнение (6.2), то получится как раз развитая в прошлой лекции более общая модель (5.3):

СL^d(W/P(R), R,...) = YL^s(W/P(R))

или

С^d(R,...) = Y^s(R)

Чтобы убедиться в этом, продифференцируем функцию спроса на товары и функцию предложения товаров по переменной R и проанализируем их на знак:

dCL^d/dR= ¶CL^d/¶(W/P)*d(W/P)/dR + ¶CL^d/¶R <0

dYL^s/dR= dYL^s/dWP*d(W/P)/dR >0.

Это и означает, что модель (6.1)-(6.2) являются развитием одного уравнения (5.3), изученного на предыдущей лекции:

С^d(R,...) = Y^s(R)

                 (-)             (+)

Данный факт, в свою очередь, позволяет заключить, что те выводы, которые ранее были сделаны относительно товарных рынков, в смысле их реакции на различные шоки предложения, остаются в силе и для более сложной модели. Выделение в ее составе рынка труда позволяет расширить анализ и вовлечь в него изучение соответствующих переменных - занятости и реальной ставки заработной платы; но если задача стоит более узко и ограничивается лишь анализом трех рынков (не включая рынка труда), возможно и обосновано использование упрощенной, более агрегированной модели (5.3).