Как мы уже знаем, если домохозяйство не может в данный период времени потратить средств больше, чем оно имеет, то это говорит о наличии у него жесткого бюджетного ограничения[11]. Возможность заимствования денег делает бюджетное ограничение почти жестким. Данный факт означает, что взятые в текущий период займы, позволяющие увеличить потребление сверх уровня заработка, в дальнейшем необходимо отдать за счет средств, которые требуется заработать. В нашем случае бюджетное ограничение для периода t выглядит следующим образом:
P×yt+bt-1×(1+R)+mt-1=P×ct+bt+mt
В левой части данного уравнения стоит сумма всех имеющихся средств - заработок, активы, приносящие доход, а также остатки денег с предыдущего периода. В правой части - направления их расходования - закупка потребительских благ, покупка активов, приносящих доход и остаток денег на конец данного периода времени.
Определим понятие сбережений в форме ценных бумаг для представительного домашнего хозяйства как bt-bt-1. В целом для закрытой экономики имеет место: Bt-Bt-1 =0. Все финансовые активы данного агента составляют: bt+mt, а в экономике в целом Mt=M. Изменение финансовых активов отдельного агента равно (mt+bt)-(mt-1+bt-1). Это и есть сбережения в номинальной форме (или по-другому - прирост финансовых активов):
(bt+mt)-(bt-1+mt-1) = P×yt+bt-1×R-P×ct
В целом в экономике в силу сформулированных выше условий - отсутствия инфляции, однородности товаров и закрытого характера экономической системы - имеет место:
P×Yt = P×Ct.
Равенство производства и потребления на товарном рынке.
4.2 Межвременной выбор: модель Фишера для двух периодов
4.2.1 Межвременное бюджетное ограничение для двух периодов.
Перейдем к анализу двухпериодной модели; при этом общий подход заключается в том, что первый из рассматриваемых периодов трактуется как текущий период времени, а второй, как и все последующие - как будущее (или просто как настоящее и будущее). Для репрезентативного домохозяйства, т.е. такого, что mt=mt-1 (поскольку Mt=const) бюджетные ограничения периодов 1 и 2 можно записать в следующем виде:
P×y1+b0×(1+R) = P×c1 + b1
P×y2+b1×(1+R) = P×c2 + b2
Выразим b1 из второго уравнения:
b1 = P×ct/(1+R) + b2/(1+R) - P×y2/(1+R).
и подставим в первое:
[P×y1+ P×y2/(1+R)] +b0×(1+R)=[P×c1 + P×c2/(1+R)] + b2/(1+R)
Обратим внимание, что слева в квадратных скобках стоит текущая стоимость дохода, а справа также в квадратных скобках - текущая стоимость потребления. И доходы, и расходы будущих периодов оцениваются с позиций текущего периода как более дешевые в виду того, что альтернативой потреблению "сегодня" является выдача кредита и увеличение потребления "завтра". Коэффициент 1/(1+R) есть коэффициент дисконтирования (дисконт), имеющий смысл цены потребления (или дохода) следующего периода, с позиций текущего периода.
Для целей дальнейшего анализа нам лучше перейти к реальным показателям, поделив предыдущее уравнение на P. Одновременно сделав преобразования, получим:
D=y1+y2/(1+R) +b0×(1+R)/P-b2/[(1+R)×P]=c1+c2/(1+R),
или c1+c2/(1+R)=D. Dесть вся та сумма реального дохода, представленная своей текущей стоимостью, которая может быть использована для потребления. Меняя величину сбережений первого периода b1 можно менять соотношение между объемами потребления в оба периода - c1, c2.Таким образом, в первый период времени выбор осуществляется между потреблением и сбережением данного периода.
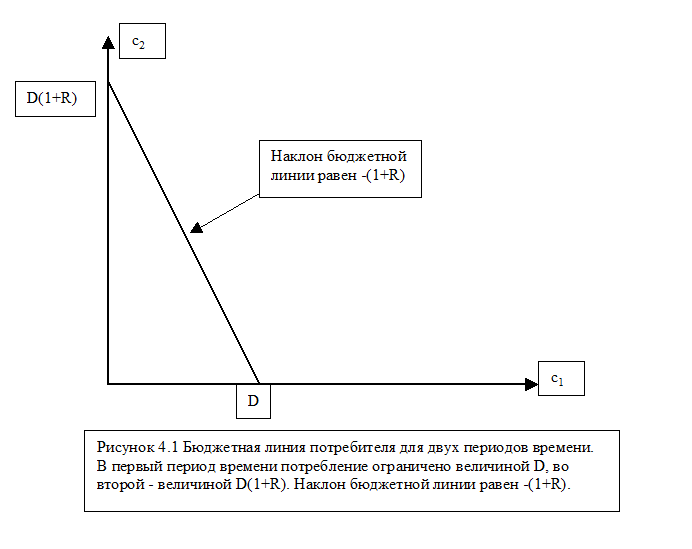 |
На графике (см. Рис. 4.1) изображена бюджетная линия для двух периодов. Точка пересечения ее с осью абсцисс составляет величину D, а с осью ординат - D×(1+R), наклон ее равен -(1+R). Выразим из данного уравнения объем потребления второго периода:
с2 = D×(1+R) - c1×(1+R).
Тогда dc2/dc1=-(1+R). Это значит, что, жертвуя в первом периоде единицу потребления, рассматриваемый потребитель во второй период получает компенсацию, измеряемую величиной 1+R. Другими словами, указанная величина является альтернативной стоимостью потребления первого периода.
4.2.2 Предпочтения: функция полезности для двух периодов
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.