Для моделирования процессов, протекающих при разработке нефтяных и газовых (в том числе и газоконденсатных) месторождений, необходимо обеспечить на модели следующие пять условий подобия [122].
1. Условие
геометрического подобия, требующее подобия
модели и
прототипа в отношении геометрических размеров.
2. Условие
кинематического подобия, требующее, чтобы со
ответствующие
частицы при движении в геометрически подоб
ных
системах описывали геометрически подобные пути.
3. Условие динамического
подобия, требующее равенства
отношения
сил одного и того же типа, действующих на соот
ветствующие
частицы в геометрически подобных системах.
4. Условие теплового
подобия, которое требует сохранения
постоянства отношения соответствующей разности температур
в геометрически и кинематически подобных системах.
5. Условие химического
подобия, требующее сохранения
постоянства
отношения соответствующей разности концентра
ций в геометрически и кинематически подобных системах.
Для постановки экспериментов в лабораторных условиях с
36
учетом условий подобия необходимо знать характеристику процесса и составить систему определяющих критериев подобия.
Наиболее полно критерии подобия для случаев вытеснения нефти и газа водой на моделях однородных и неоднородных пористых сред, в том числе и на моделях слоистых пластов, рассмотрены в работах [25, 58, 73, 78, 99, 112, 113].
Применительно к вытеснению нефти водой из трещиновато-пористой модели авторами [17, 57] показано, что в общем случае процесс вытеснения определяется параметрами jui, 112, о, v, L, 0, k, т, Ар, 6, Н. Здесь щ, \л2 — коэффициенты динамической вязкости нефти и воды соответственно; v — скорость вытеснения нефти водой; L — длина пористого блока матрицы; Н — половина ширины блока; о — коэффициент поверхностного натяжения; Э — угол избирательного смачивания; т — коэффициент пористости блока; k — коэффициент проницаемости блока; Ар — разность плотностей вытесняющей и вытесняемой жидкостей; 6 — раскрытие трещины.
Из этих параметров авторы составляют восемь независимых безразмерных параметров:
= L/H, П3 =
jt4 = ~[/k IH, пъ = cos 0, jt6 = m, jt7 = Apgk/vyLlf n8 = k/6.
Путем комбинации указанных параметров получен параметр a cos QL
' __ а cos QL ykjm < j g\
Этот параметр по физическому смыслу представляет собой отношение градиента капиллярных сил в направлении ширины модели Я к градиенту гидродинамических сил в направлении длины модели L.
Маттакс и Кайт [135] доказали экспериментально, что для одного и того же отношения вязкостей вытесняющей и вытесняемой жидкостей и при геометрическом подобии размеров пористых сред текущий коэффициент вытеснения нефти водой определяется безразмерным параметром
![]() ta cos 9 Л/kjm
ta cos 9 Л/kjm
п =--------- ]ф---------
Нетрудно видеть, что параметр л0 вытекает из п\, так как L/v имеет размерность времени.
Если предположить, что в пористом блоке давление остается неизменным, то коэффициент вытеснения газа водой будет также определяться безразмерным параметром ло. В связи с этим результаты описанных экспериментов были обработаны в
37
 180 200
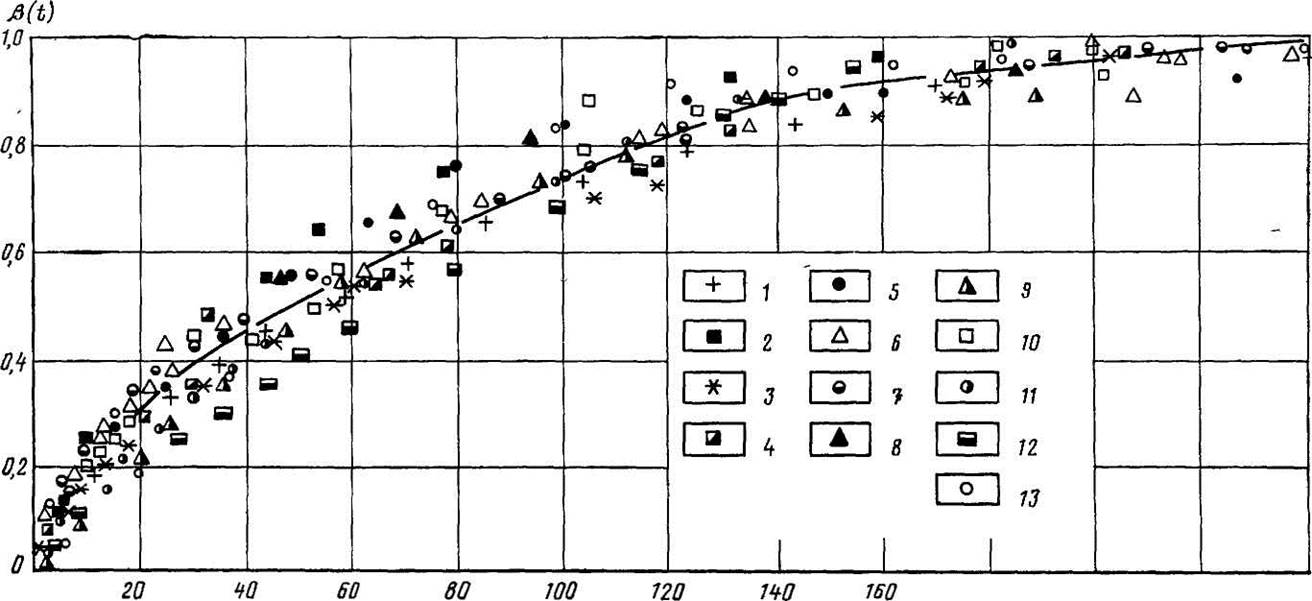
220 я0 Рис.
16. Критериальная обработка результатов экспериментов по
прямоточной капиллярной пропитке.
180 200
220 я0 Рис.
16. Критериальная обработка результатов экспериментов по
прямоточной капиллярной пропитке.
Образец: / —1; 2-7; 3-12; 4—14; 5-16; 6-17; 7-18; 8-19; 9 — 22; /0 — 24; 11 — 1755,3; /2-1808; /3-1881
|
|
Рис. 17. Зависимость текущего значения коэффициента вытеснения от безразмерного параметра Ко-
|
р 13— 1881 |
Образец- /- 1; 2-7; 3- 12; 4-14; 5-16; 6-17; 7- 18; 8- 19; 9-22; /0-24; /^ — 1755,3; 12- 1808; 13 1881
координатах р(/)~я0. Из рис. 16 следует, что независимо от размеров блоков, коэффициентов пористости и проницаемости прослеживается довольно четкая'зависимость р(£) =f (я0).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.