Приемно-передающие устройства радио­технических систем: Учебное пособие, страница 71

большей развязкой как между отдельными входными, так и меж­ду входными и выходньвмн цепями. При включении нагрузки в об­щую эмиттерную цепь (рис. 5.19,в) еухмматор обладает наиболь­шей нагрузочной способностью и не изменяет полярности сигналов па выходе, однако имеет по каждому входу низкий коэффициент передачи по напряжению (Kui,2<l)-

Для обеспечения устойчивости функционирования адаптивных систем с корреляционными обратными связями при большой ин­тенсивности помехоных колебаний часто в контур управления включают АРУ или ограничители с фиксированным или управля­емым уровнем ограничения. Путем управления уровнем ограниче­ния можно регулировать время адаптации, обеспечивая устойчи­вость функционирования системы адаптации. Ограничитель влияет на функционирование системы адаптации только в переходном ре­жиме и не влияет на ее работу в установившемся режиме [9].

Все адаптивные системы, основанные на прямых методах вычис­
ления весовых коэффициентов, как правило, реализуются цифро­
выми устройствами (спецвычислителями). При их технической ре-
ализиции основное внимание обращается на качественное преоб­
разование аналоговых сигналов в цифровую форму (см. разд. 2)
и на выбор алгоритма вычисления вектора весовых коэффициен­
тов, обеспечивающего устойчивость функционирования системы
при ограниченной разрядности спецвычислителя и требуемое
быстродействие.                                                               •    i

286

5.3.4. Эффективность компенсации помех при наличии нестабильностей параметров приемных каналов

Получение соотношений, связывающих качество пространствен­ной обработки с параметрами многоканальных приемных уст­ройств, является довольно сложной задачей. Поэтому предвари­тельно рассмотрим вопрос подавления помехи только для однока-нального пространственного фильтра. Как известно, коэффициент подавления помехи дя этого случая определяется 'выражением [2]

где рл —коэффициент взаимной корреляции помеховых сигналов на выходах основного и дополнительного каналов приема. Как видно из этого -выражения, для эффективного подавления помехи необходимо иметь /pj/, близкое ¹к единице.

Коэффициент корреляции зависит от многих факторов. К ним, в первую очередь, относятся:

неидентичности амплитудно-частотных и фазо-частотных харак­теристик приемных каналов, характеризуемые коэффициентом кор­реляции (Рнеид):

различие нелинейностей приемных каналов (р_нел);

отношение помеха/шум на выходе приемных каналов (р _п/ш);

различие задержек огибающей помехи в каналах приема (рдт).

Общий коэффициент корреляции определяется как произведе­ние частных коэффициентов корреляций, вызванных отдельными нестабильностями и неидентичностями,

где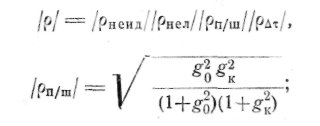

ёо> §к —отношение мощности помехи к мощности внутренне­го шума в основном и компенсационном каналах соответственно;

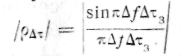 — для прямоугольного спектра    помеховых ко -

лебаний;

Д/ — ширина спектра помеховых колебаний;

&х_а =/%₃₀ — т_зк/ —разность задержек огибающей помехи между каналами приема.

Соотношения для /рнел, и /рнеид/невозможно выразить просты­ми 'Соотношениями. Их оценки можно получить из кривых графи­ков, представленных в работах [10, 11].

На коэффициент подавления помехи оказывает значительное влияние точность вычисления и установки весового коэффициента.

где— характеризует точность    установки модульного

значения весового вектора;

г₀ — точное значение весового вектора;

Лг — амплитудная  погрешность установки  весового вектора;

Лф — фазовая погрешность установки весового вектора. Тогда подставив

/р>/ = IpIIp»i

в выражение для коэффициента подавления помехи, можно опре- J делить   влияние   нестабильностей   параметров   приемных   каналов на качество подавления номеховых колебаний.

Точность вычисления и установки весовых коэффициентов для многоканальных адаптивных систем оценим по остаточной мощ­ности помех на выходе адаптивной системы. Известно, что при установке оптимального весового вектора остаточная мощность помех определяется выражением [2]

Из-за неточности вычисления весового вектора и его установки весовой вектор отличается от оптимального и может быть пред­ставлен в виде [12]

К = Копт    I    ^с,

где S — вектор 'случайных ошибок. Тогда

Можно полагать, что между .каналами случайные ошибки незави­симы М(8Д) —0, имеют нулевые средние значения М(8,)==0, a каналы статистически однородны M{b-fii) — о а. Тогда средняя мощность ломеховых колебаний на выходе адаптивной системы будет равна

где .Бр(Ф) —след корреляционной матрицы помех.

Введем   коэффициент   затрубления   чувствительности   адаптив­ной системы из-за неточности вычисления весовых коэффициентов

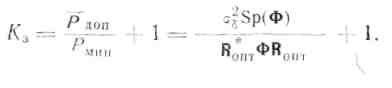
Для  адаптивной системы с равноценными приемными каналами последнее выражение преобразуется к виду

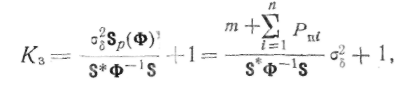
где Рш —относительная мощность г'-го источника помехи в каж­дом приемном канале.

Полученное соотношение показывает, во сколько раз увеличи­вается мощность 'остатков помех на выходе адаптивной приемной системы при наличии ошибок в вычислении и установке весо­вых коэффициентов.

Пример.

Определить длину разрядной сетки кода управления квадра­турными весовыми регуляторами (рис. 5.14,а), если допускается увеличение мощности остатков помех за счет ограничения разряд­ной сетки кода управления аттенюаторами 1дБ, ЗдБ и 5дБ.

Решение.

Дисперсия ошибки кода управления определяется ценой млад­шего разряда Л_г кода управления, т. е.

Тогда

а с учетом того, что для пассивных весовых регуляторов    /f</~l» т. е. A_r ~ —jzr    V~~число разрядов кода управления), имеем

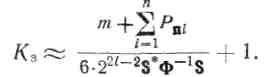
Из этого выражения можно получить требуемое число разрядов кода управления при заданном уровне Кз

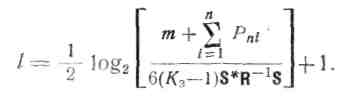
Результаты расчетов приведены в виде графиков на рис. 5.20. Влияние неидентичностей частотных характеристик приемных каналов на качество подавления помех, а также проблемы обра­ботки широкополосных пространственно-временных сигналов в виду сложности их рассмотрения для многоканальных адаптивных