Приемно-передающие устройства радио­технических систем: Учебное пособие, страница 43

Такая форма позволяет представить 2^L+1 различных чисел (2^L отличающихся во абсолютной величине чисел с шагом 2^-L). Если результат арифметической операции выходит за верхний предел неравенства (3.29), то происходит переполнение разрядной сетки, приводящее к искажению результата. При согласованной фильтрации такое переполнение может, например, возникнуть, если не будет учтено возможное увеличение в М раз уровня сигна­ла на выходе фильтра по сравнению с его входным сигналом.

Проблема динамического диапазона практически не возникает при использовании способа с плавающей запятой, так как для ее решения достаточно добавить один-два дополнительных разряда в порядок числа. Однако техническая реализация цифрового фильт­ра при таком представлении усложняется, а также уменьшается его быстродействие. Причиной этого является необходимость пред­варительного выравнивания порядков чисел при сложении с по­следующей нормализацией результата, а при умножении — необ­ходимость выполнения двух операций: перемножения мантис и сложения порядков. Кроме того, при представлении чисел с пла­вающей запятой будет вноситься ошибка не только при выполне­нии операций умножения, но и сложения, так как в ходе нормали­зации часть разрядов одного из чисел теряется.

Учитывая вышеизложенное, особенно более высокое быстро­действие, при обработке радиолокационных сигналов шире применяется способ представления чисел с фиксированной запятой, как правило, в дополнительном коде. Разрядность всех матричных ум­ножителей (рис. 3.19) одинакова, при этом число разрядов произ­ведения, как правило, округляется до разрядности представления входного сигнала путем отбрасывания младших разрядов и, при необходимости, добавления единицы в последний разряд. В отли­чие от умножителей разрядность сумматоров АУ нарастает с уве­личением числа регистров по закону log₂M. Например, при М = 64 разрядность последнего сумматора АУ должна быть на 6 больше, чем у АЦП.

Произведения, полученные на выходе арифметических уст­ройств АУ1...АУ4, суммируются с учетом знака в соответствии с алгоритмом (3.27). Параллельные двоичные коды реальной и мни­мой частей корреляционного интеграла с выходов сумматоров  поступают на устройство вычисления модуля, называ­емое иногда «цифровым амплитудным детектором». На практике, как правило, используются приближенные методы вычисления мо­дуля , что связано со сложностью техничес­кой реализации данной операции как на аналоговой, так и на циф­ровой элементной базе. Рассмотрим один из приближенных алго­ритмов вычисления модуля, называемый алгоритмом Робертсона. Для этого обозначим      R и вначале предположим, что А>В. Тогда по формуле бинома Ньютона получаем

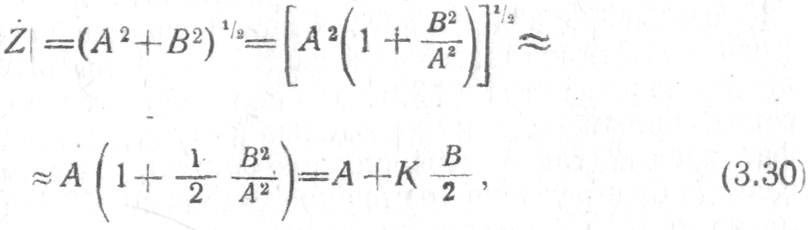
где .

Очевидно, что погрешность данного алгоритма зависит от от­ношения В/А, а ее максимальное значение будет при В/А = 1. Оп­ределим величину максимальной относительной погрешности при­ближенного вычисления

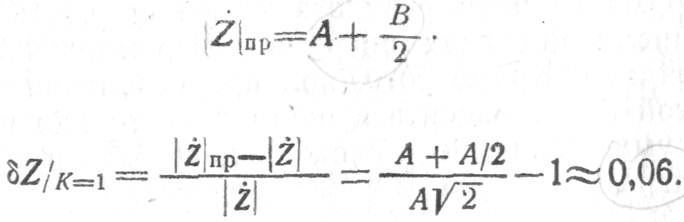
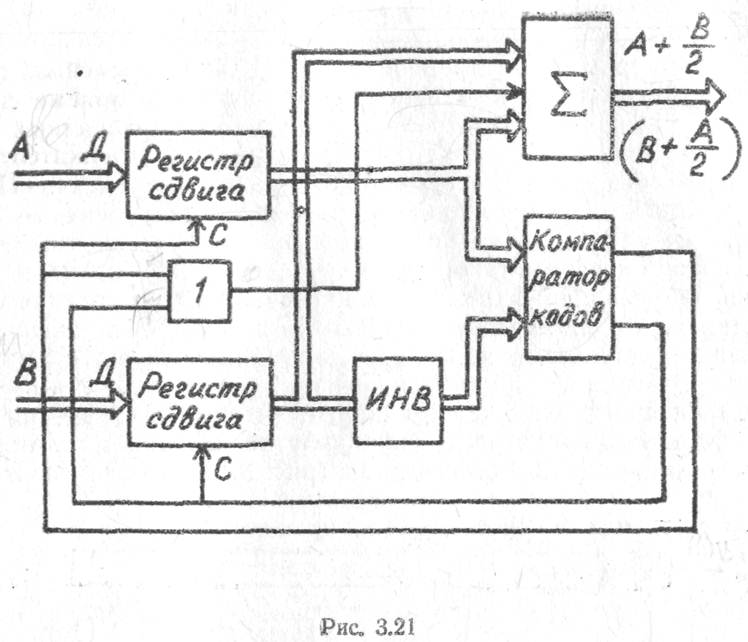
Итак, максимальная погрешность данного алгоритма составля­ет около 6%. Заметим, что противоположное предположение В>Адает приближенный алгоритм в виде . Поэтому схе­ма рис. 3.21, реализующая данный алгоритм, содержит компара­тор кодов, сравнивающий коды реальной и мнимой части . В за­висимости от результата сравнения компаратор кодов вырабаты­вает импульс сдвига С, сдвигающий код реальной либо мнимой части на один разряд вправо в соответствующем регистре сдви­га, после чего параллельный сумматор реализует операцию при­ближенного алгоритма.

Иногда для дальнейшего упрощения алгоритма вычисления  производят отбор максимального значения кода , что приводит к потерям в пороговом сигнале, не превышающем 0,7 дБ [10].

В ряде случаев наряду с вычислением при цифровой обра­ботке сигналов необходимо произвести вычисление фазы корреля­ционной суммы

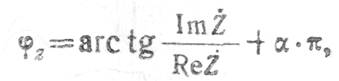
где

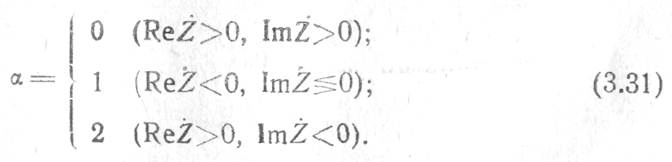
Использование для вычисления  простых аппроксимирую­щих выражений функции «arc tg» недопустимо ввиду больших оши­бок аппроксимации. Поэтому одним из способов технической реа­лизации вычислителя  является применение ПЗУ, в ячейках па­мяти которого хранятся все возможные значения  от 0° до 90°. Требуемая дискретность значений qi_z обеспечивается выбором микросхемы ПЗУ с достаточными объемом памяти и разрядностью хранимых в памяти чисел. Адресами ПЗУ являются цифровые ко­ды значений . Данная схема должна быть дополнена схемой вычисления а в соответствии с алгоритмом (3.31). Необходимо отметить, что подобный метод с использованием ПЗУ может быть применен и для нахождения .

Недостатком рассмотренной схемы ЦСФ во временной области (рис. 3.19) является ее сложность, особенно при приеме сигналов с большой, когда требуемое число многоразрядных регист­ров, сумматоров, и самое главное, матричных умножителей равное  составляет сотни и даже тысячи. Поэтом на практике иногда находят применение нерекурсивные ЦСФ бинарным квантованием комплексной амплитуды входного сигна­ла. Отличием схемы такого фильтра от рис. 3.19 является приме­нение одноразрядных регистров и переход от умножения в соответствии с (3.27) параллельных кодов в МУ к суммированию тех значений импульсной характеристики, для которых имеется еди­ничная выборка принимаемого сигнала.

Дальнейшим упрощением является аналого-цифровая схема согласованного фильтра с бинарным квантованием комплексной амплитуды принимаемого сигнала (рис. 3.22). После фазового детектирования

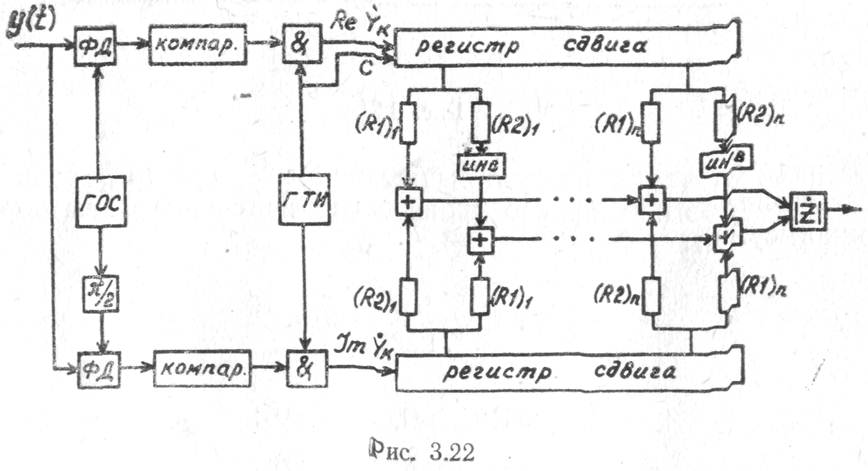
принимаемого сигнала в двух квадратурных подканалах с помощью генераторов гармонических опорных сигналов ГОС, амплитудного квантования на два уровня (0,1) в компара­торе и временной дискретизации в схеме совпадения с тактовой частотой генератора тактовых импульсов ГТИ временные выбор­ки , заполняют разряды соответствующих регистров сдвига. Умножение временных выборок на комплексную импульс­ную характеристику согласованного фильтра (3.27) осуществля­ется путем деления выходных напряжений триггеров регистров сдвига в делителях, состоящих из прецизионных резисторов   и входных сопротивлений  сумматоров

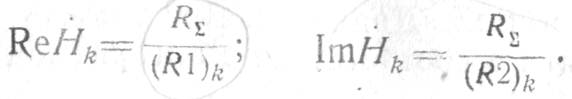
Например, для согласованной фильтрации простого радиоимпульса с доплеровской частотой .