Для определения предельной чувствительности Рпред корреляционного либо корреляционно-фильтрового РПрУ воспользуемся выражением для отношения сигнал-шум на выходе коррелятора [27]
Где 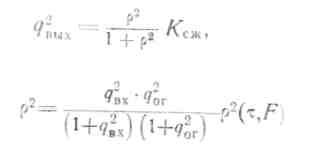 (3.53)
(3.53)
- коэффициент корреляции входных и гетеродинных колебаний (рис. 3.40);
q2вх и q2ог — отношения сигнал-шум по мощности на входах коррелятора;
ρ2(τ, F) — время-частотная функция рассогласования принимаемых и гетеродинных сигналов [1]:
Ксж = Δfс• τсэ — коэффициент сжатия полезного сигнала по спектру.
Для определения предельной чувствительности примем два предположения, выполняющиеся на практике: q2вх « 1, q2ог » 1. Тогда из (3.53) следует, что ρ2 ≈ q2вх • ρ2(τ, F), a q2вых = q2вх •Ксж• ρ2(τ, F). Руководствуясь определением Рпред, из условия q2вых= 1 с учетом энергетических потерь при обработке получаем
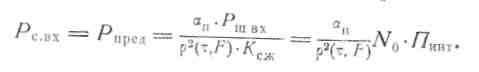
Сравнение данного выражения с формулой предельной чувствительности фильтрового приемного устройства (3.11) показывает, что с учетом (3.52) при τ=0 и F=0 они совпадают, хотя преобразования сигналов в корреляционном и фильтровом приемниках существенно отличаются.
Величина αп в корреляционном (корреляционно-фильтровом) приемном устройстве в основном определяется частотными расстройками гетеродинов приемника, его резонансного тракта, особенно стабильностью настройки интегрирующих фильтров. Поэтому в резонансных цепях таких приемников, как правило, применяются фильтры с высокой механической прочностью и температурной стабильностью (фильтры на ПАВ, кварцевые, электромеханические фильтры и др.), для которых величина потерь αп, возникающих ввиду изменения полосы пропускания и формы АЧХ, а так-
204
же резонансной частоты широкополосного приемного тракта, рас положенного до перемножителя коррелятора, составляет менее 1 дБ [15]..
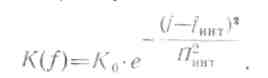
Учитывая, что Δfгет i < Пинт , представим амплитуду напряжения на выходе интегрирующего фильтра в виде
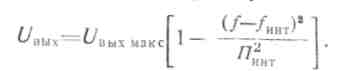
Из данного выражения следует, что в случае независимых уходов частоты гетеродинов
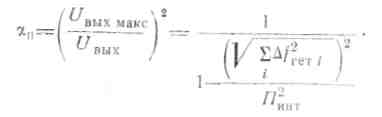
Влияние на величину αп нестабильностей частоты гетеродинов Δfгет i рассмотрим на примере корреляционного приемника с бесконечно малой шириной спектра сжатого сигнала интегрирующим фильтром, имеющим гауссову АЧХ
Последнее соотношение говорит о том, что при среднеквадратическом значении нестабильности частоты гетеродинов, составляющем 0,5 Пинт, αп достигает более 1 дБ.
Значительные потери в отношении сигнал-шум на выходе коррелятора возникают при декорреляции сигналов обобщенного гетеродина и принимаемых сигналов, вызванной нелинейными искажениями последних в приемном тракте. Такие искажения возникают при установке в нем амплитудного ограничителя с целью расширения узкого динамического диапазона перемножителя коррелятора. При этом отношение сигнал-шум по мощности на выходе ограничителя q2огр будет равно [14].
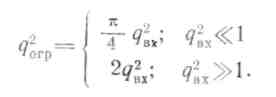 (3.55)
(3.55)
Из данных соотношений и выражения (3.53) следует, что в наиболее тяжелом случае q2вх «1 потери αп = 4/π, т.е. около 1 дБ.
Энергетические потери несколько возрастают при переходе от аналоговой корреляционной обработки к цифровой. Как и в случае цифровой согласованной фильтрации, цифровая корреляционная обработка в реальном масштабе времени возможна лишь для
205
сравнительно узкополосных сигналов (единицы МГц), причем даже в этом случае схема многоразрядного цифрового коррелятор;, получается столь же сложной, как и ЦСФ (рис. 3.19).
Упрощение схемы цифрового коррелятора может быть достигнуто при грубом амплитудном квантовании одного или обоих перемножаемых сигналов на 3...5 или 2 уровня в так называемых корреляторах Стилтьеса, релейных и знаковых (полярных) корреляторах [18]. Последние нашли на практике наиболее широкое при менение ввиду простоты вычисления знаковой корреляционной функции
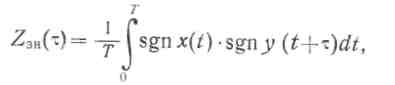 (3.56)
(3.56)
Где

Учитывая, что закон распределения принимаемого сигнала непрерывный, т. е. Р(х = 0) =Р(у=0) =0, при цифровой технической реализации целесообразно от 3-уровневого представления знаковой функции signx(t) перейти к 2-уровневому:
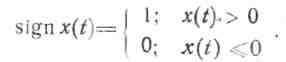
|
|
|
где Y и X— коплексные амплитуды напряжений сигнала и обобщенного гетеродина; |
|
|
|
— период временной дискретизации принимаемого |
Тогда выражение (3.56) после нормировки представляется в виде суммы [16]
сигнала;
N — число временных выборок сигнала, по которым производится вычисление знакового коэффициента корреляции;
Ө— операция суммирования по модулю 2.
Из выражения (3.57) следует, что цифровой знаковый коррелятор вычисляет вероятность совпадения знаков принимаемого сигнала и колебаний обобщенного гетеродина, сдвинутых друг относительно друга на интервал кТт. В частности
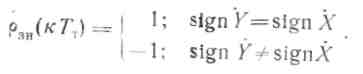
206
Лишь в том случае, когда число совпадений и несовпадений знаков одинаковы, ρзн (кTт) = 0. Структурная схема цифрового знакового коррелятора представлена на рис. 3.44.
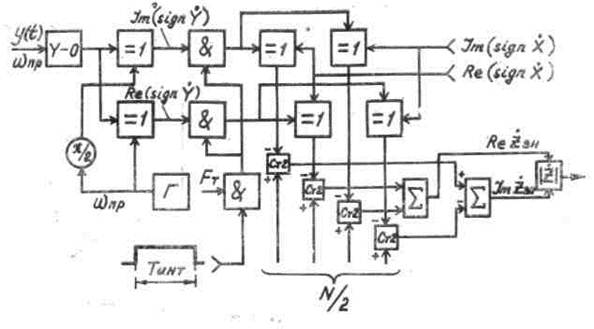
Рис. 3.44
Входной усилитель-ограничитель (Y - 0) за счет значительного усиления обеспечивает преобразование входного сигнала в сигнум-сигнал. Схемы «исключающее ИЛИ», расположенные на входах двух квадратурных каналов, совместно с генератором Г опорного гармонического колебания обеспечивают преобразование спектра сигнум-сигнала в область видеочастот, необходимое для понижения частоты временной дискретизации .FT. Ввиду комплексного представления сигналов У и X операция суммирования по модулю 2 (3.57) производится в четырех ИМС «исключающее ИЛИ».
Единичные импульсы, возникающие на их выходах при несовпадении полярностей ис и иог, поступают на вычитающие входы реверсивных двоичных счетчиков, в которые перед каждым циклом накопления предварительно записывается число N/2 (3.57). Число разрядов счетчика «л» должно быть не менее log2Kсж, например, при Тинт=100 мкс, Δfс = 10 МГц и ТТ = 1/4Δfс получаем «=12. После суммирования в сумматорах параллельных кодов, соответствующих реальной и мнимой части Z3H, производится вычисление модуля знаковой корреляционной функции (рис. 3.21).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.