Приемно-передающие устройства радио­технических систем: Учебное пособие, страница 5

Элементы матрицы связаны с величинами, определяемыми из­мерительными приборами на СВЧ, что позволяет составлять рас­четные и экспериментальные характеристики линейных каска­дов. Таким образом, анализ линейных каскадов возможен при использовании любой системы внутренних параметров четырех­полюсника. При этом знание параметров в какой-либо системе позволяет однозначно перейти к любой другой системе парамет­ров. При расчете внешних параметров линейных каскадов (тех­нических параметров или технических показателей) предпочтение отдается использованию параметров, которые можно измерить непосредственно в том диапазоне частот, в котором работает кас­кад радиоприемного устройства. К техническим параметрам, ха­рактеризующим усилительные и шумовые свойства линейных кас­кадов, относятся:

коэффициенты усиления передачи напряжения, тока и мощ­ности;

входная и выходная проводимости (входное и выходное со­противления);

коэффициенты отражения на входе и выходе;

коэффициент   шума,   или  шумовая  температура.

Определение перечисленных параметров производится по ста­тическим параметрам эквивалентного четырехполюсника в лю­бой системе параметров (У, Z и S) >и известным характеристи­кам источника сигнала и нагрузки. Преимущественное использо­вание той или иной системы и группа основных технических па­раметров определяются диапазоном частот, в котором работает каскад, и его предназначением.

Так, для усилителей высокой частоты такими параметрами являются коэффициент передачи номинальной мощности, коэф­фициент шума, полоса пропускания, избирательность. В метро­вом и дециметровом диапазонах волн, в которых измерительные приборы градуируются в единицах напряжения, к основному па­раметру УВЧ относят также коэффициент 'передачи напряжения. Эта же группа параметров характеризует свойства предваритель­ных усилителей промежуточной частоты.

Для усилителей промежуточной частоты основными техничес­кими параметрами являются коэффициент усиления напряжения, полоса пропускания, избирательность, предельный коэффициент устойчивого усиления на один каскад. Остальные параметры, как правило, являются вспомогательными.

Технические параметры линейных каскадов через статические Y-параметры определяются следующим образом.

1. Коэффициент усиления напряжения каскада К_и равен от­ношению напряжений на входных и выходных зажимах эквива­лентного четырехполюсника (рис. 1.10)

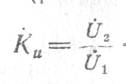
Воспользовавшись уравнениями  (1.1) и  (1.2), получим

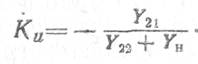
2. Коэффициент усиления тока

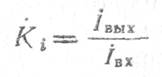
где i_вых— ток короткого замыкания на выходе, равный

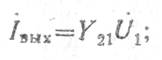
i_вх — полный ток источника через проводимости Y_c и Y₁₁

Тогда

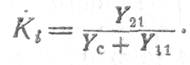
3. Входная проводимость

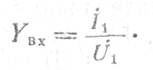
С учетом  использования первого уравнения   (1.1)   и выраже­ния для К_и получим

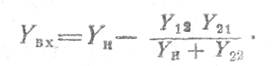
4. Выходная проводимость

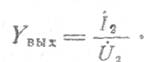
Используя второе уравнение  (1.1), получим

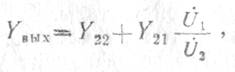
где отношение напряжении      —  имеет смысл коэффициента передачи напряжения с выхода каскада на его вход. Подставим в него уравнение, выражающее i_вх для эквивалентного генератора вносимого тока

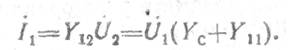
Тогда 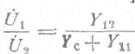 и зависимость для выходной проводимости

принимает вид

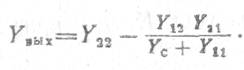
5. Коэффициент усиления мощности линейного   каскада Kр в общем случае равен

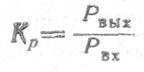
Представляет интерес максимальный коэффициент усиления при согласовании на входе g_c= g_вх и выходе каскада g_н= g_вых. При этих условиях номинальные мощности на входе и выходе равны:

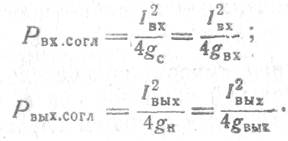
Тогда с учетом выражения для Ki

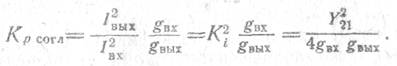
6. Коэффициент шума каскада равен

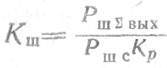
Так как

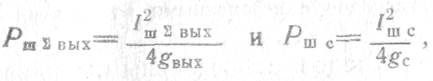
то

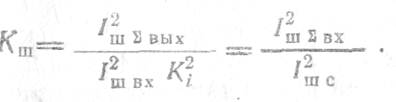
Следовательно,  коэффициент шума  может быть найден    как отношение среднего квадрата токов всех источников I²_ш∑,   пересчитанных на вход каскада, к среднему квадрату шумового тока источника сигнала I²_{Ш с} .

7. Предельный коэффициент усиления каскада

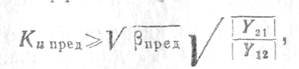
где βпред — предельный параметр регенерации. Для идентичных каскадов

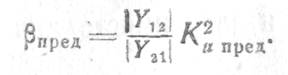
Впервые   выражения   для   К_ипредпри β=0 было получено В. И. Сифоровым

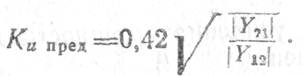
8. Полоса   пропускания усилительного каскада    определяется амплитудно-частотной    характеристикой    резонансной    нагрузки

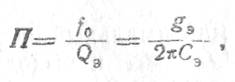
где 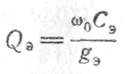 - эквивалентная    добротность    колебательной

системы;

С_э — эквивалентная емкость колебательной системы.

Наличие положительной обратной связи в каскаде уменьшает полосу пропускания. Поэтому в общем случае

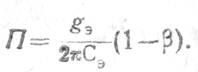
Таким образом, при выборе коэффициента усиления каскада, равным K_{u пред}, его полоса пропускания уменьшается примерно на   20%.

Приведенные в данном разделе соотношения используются при анализе конкретных схем линейных каскадов приемных и передающих устройств.

1.2.2. Анализ  линейных  каскадов  с  переменными  во  времени  параметрами

Кроме линейных каскадов с постоянными параметрами, в приемно-передающих системах используются устройства, анализ работы которых при помощи теории линейных каскадов не всегда является правомерным. Это относится, прежде всего, к малошумящим параметрическим и квантово-механическим регенератив­ным усилителям, в которых энергия на компенсацию потерь   потребляется не только от источников постоянного тока, вои от высокочастотных источников. Поэтому необходимо учитывать свойства нелинейных элементов, учитывающих в механизме ко­герентной передачи энергии от источника к сигналу.

Теория линейного шумящего каскада может быть использо­вана и для других каскадов приемно-передающего тракта, осу­ществляющих необходимые операции обработки сигнала, такие, как перенос его спектра из одной области в другую (преобразо­вание частоты), детектирование, модуляцию, перемножение ам­плитуд и свертку радиосигналов, а также сжатие динамического диапазона путем регулирования усиления и т. д.

Все эти операции над сигналом могут быть произведены при помощи цепей с изменяющимися «во времени параметрами. В большинстве случаев такие цепи представляют собой шестиполюсники с двумя входами и одним выходом.

При некоторых ограничениях шестиполюсники с нелинейными элементами могут быть представлены для напряжения сигнала как линейные четырехполюсники с переменными параметрами.

Особенностью этих каскадов является то, что при относитель­но малом входном сигнале у них сохраняется линейная зависи­мость между огибающими амплитуд входного и выходного сиг­налов.