Для согласованной фильтрации полученный
спектр принимаемого сигнала G(f) (рис. 3.13) умножается на известную частотную
характеристику ![]() .
Операция умножения, как правило, реализуется в балансных схемах
перемножителей (смесителей либо модуляторов).
.
Операция умножения, как правило, реализуется в балансных схемах
перемножителей (смесителей либо модуляторов).
Легко показать, что для реализации устройства ОПФ, т. е. восстановления корреляционного интеграла по его спектру, может быть использована та же схема рис. 3.14,а, но имеющая ЛЧМ, гетеродин с обратным знаком изменения частоты (знаки в показателях степени (3.13) и (3.14) необходимо изменить на противоположные). Однако в ряде случаев нет необходимости в реализации ОПФ, например, в приемных трактах, осуществляющих селекцию сигналов по доплеровской поправке частоты, либо в разведывательных приемниках, осуществляющих спектральный анализ входных сигналов [3, 4].
В заключение перечислим основные требования, предъявляемые к параметрам АЭФП:
1. Для сжатия входных сигналов их длительность
![]() должна быть
согласована с длительностью импульсной характеристики ДЛЗ
должна быть
согласована с длительностью импульсной характеристики ДЛЗ
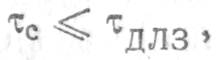
при этом период изменения частоты ЛЧМ
гетеродина может быть как равен ![]() , так и много больше
, так и много больше ![]() (скользящее ЛЧМ преобразование
[4]);
(скользящее ЛЧМ преобразование
[4]);
2. Полоса пропускания ДЛЗ
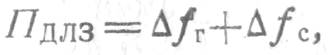
где ![]() —девиация частоты ЛЧМ гетеродина в течение
длительности сигнала;
—девиация частоты ЛЧМ гетеродина в течение
длительности сигнала;
3. Разрешающая способность по частоте при спектральном анализе определяется разрешающей способностью по времени
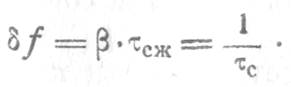
Так как дальность до цели неизвестна, то СФ на
фурье-процессорах должен работать в асинхронном режиме [4]. При этом вводится
второй канал согласованной фильтрации, в котором, как и в первом, выполняется
условие ![]() однако
начала сигналов 1-го и 2-го ЛЧМ гетеродинов сдвинуты на 0,5
однако
начала сигналов 1-го и 2-го ЛЧМ гетеродинов сдвинуты на 0,5![]() относительно соответствующих
ЛЧМ-сигналов первого канала. Результирующий сигнал СФ .получают, объединяя
выходные сигналы первого и второго каналов.
относительно соответствующих
ЛЧМ-сигналов первого канала. Результирующий сигнал СФ .получают, объединяя
выходные сигналы первого и второго каналов.
Рассмотрим особенности СФ на фурье-процессорах, реализованных с помощью ПЗС. Так как ПЗС обрабатывают дискретные сигналы, то для синтеза структуры процессора используем искусственную подстановку в показателе степени выражения для дискретного преобразования Фурье [1]:
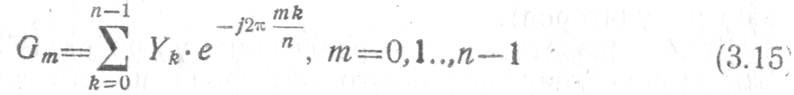
вида ![]()
В результате получаем
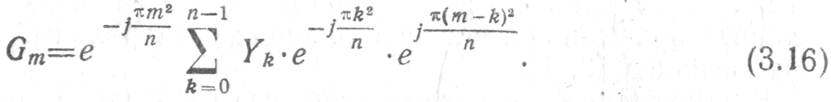
Сравнение (3.16) и (3.14) показывает, что фурье-процессор на ПЗС может быть реализован по структуре, аналогичной АЭФП (рис. 3.14). Для создания ПЗС — сжимающего фильтра его импульсная характеристика должна представлять собой ЛЧМ сигнал. Такая импульсная характеристика может быть сформирована в ПЗС-фильтрах, представленных на рис. 3.10, 3.11.
В заключение перечислим основные достоинства аналоговых и дискретных СФ на фурье-процессорах:
возможность обработки сигналов с шириной спектра в несколько десятков и даже сотен мегагерц (АЭФП) либо мегагерц ( ФП на ПЗС) в реальном масштабе времени;
простота и технологичность схемы построения;
адаптация фильтров к виду принимаемого
сигнала путем изменения закона ![]() .
.
3.2. Оценка энергетических потерь, вызванных нестабильностями характеристик согласованных фильтров
Рассогласование параметров СФ и принимаемого сигнала может быть вызвано как нестабильностями при формировании зондирующего сигнала (ч. 1 разд. 7), так и нестабильностями параметров СФ, всегда имеющими место на практике. Причинами этих искажений являются вибрации, нестабильности источников питания, эффекты старения, а также изменения температуры, влажности, давления и другие климатические факторы.
Для аналоговых СФ наиболее характерными нестабильностями являются регулярные гармонические искажения амплитудно-частотной и фазочастотной характеристик фильтра, изменение длительности его импульсной характеристики и частоты настройки, а также случайные нестабильности коэффициента передачи и фазового сдвига сигнала ;в фильтре, подчиняющиеся, как правило, нормальному закону распределения. Произведем оценку влияния регулярных гармонических искажений АЧХ я ФЧХ, представленных на рис. 3.15,
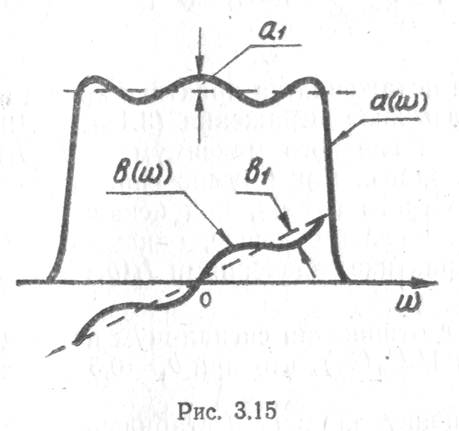
где 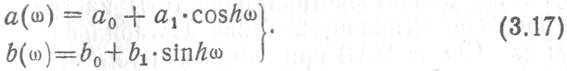
Искаженный полезный сигнал на выходе такого фильтра будет иметь вид
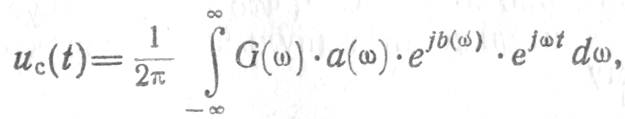
где G(![]() )
—спектр входного сигнала;
)
—спектр входного сигнала;
![]() — величина
отклонения частоты от центральной частоты настройки
— величина
отклонения частоты от центральной частоты настройки ![]() СФ.
СФ.
Подставляя в последнее выражение соотношения (3.17) и производя замены
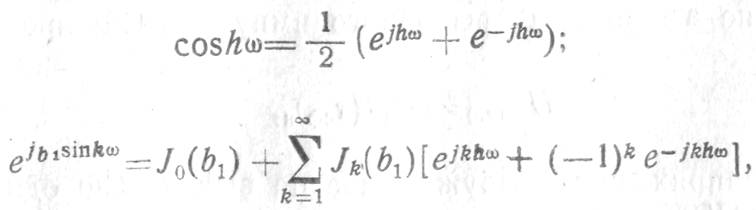
получаем:
для случая искажений только АЧХ ![]() .
.
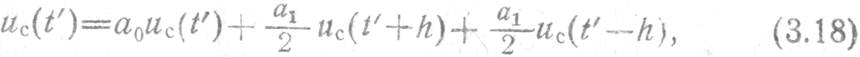
где t' = t + b0;
![]() (t') — неискаженный сигнал на выходе СФ; для случая искажений
только ФЧХ
(t') — неискаженный сигнал на выходе СФ; для случая искажений
только ФЧХ ![]()
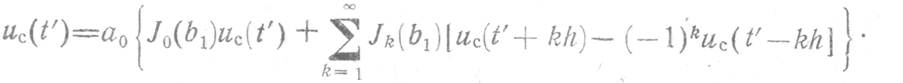
![]()
И те, и другие искажения на практике присутствуют в совокупности
и. как показывают выражения (3.18), (3.19), вызывают наряду со снижением
главного максимума в ![]() раз
появление дополнительных ложных максимумов оправа и слева от главного («парные
эхо»). Строго говоря, при искажении ФЧХ количество «парных эхо» бесконечно
большое, однако при
раз
появление дополнительных ложных максимумов оправа и слева от главного («парные
эхо»). Строго говоря, при искажении ФЧХ количество «парных эхо» бесконечно
большое, однако при ![]() рад
(что выполняется на практике) значениями
рад
(что выполняется на практике) значениями ![]() при
при ![]() можно пренебречь.
можно пренебречь.
Проигрыш ![]() в отношении сигнал-шум по мощности в
главном максимуме равен
в отношении сигнал-шум по мощности в
главном максимуме равен ![]() , что при
, что при ![]() рад составляет менее 1 дБ.
рад составляет менее 1 дБ.
Произведем оценку влияния нестабильности
длительности импульсной характеристики и частоты настройки СФ на выходное
отношение сигнал-шум. Такие нестабильности особенно характерны для СФ на ПАВ
при изменении температуры окружающей среды, что вызывает изменения длины
звукопровода и скорости ПАВ [4]. Так, например, для наиболее широкополосного
звукопровода из ниобата лития относительный температурный коэффициент задержки
равен примерно ![]() ,
что соответствует относительному изменению длительности импульсной
характеристики при
,
что соответствует относительному изменению длительности импульсной
характеристики при ![]() ,
равному
,
равному
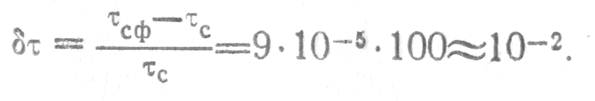
Рассмотрим влияние нестабильности длительности
![]() импульсной
характеристики для случая фильтрации простого радиоимпульса длительностью
импульсной
характеристики для случая фильтрации простого радиоимпульса длительностью ![]() . При отсутствии (искажений
максимальное значение амплитуды выходного импульса СФ представим в виде
. При отсутствии (искажений
максимальное значение амплитуды выходного импульса СФ представим в виде
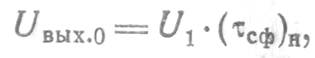
где ![]() — напряжение,
возбуждаемое на выходе СФ одной парой электродов ПЭП;
— напряжение,
возбуждаемое на выходе СФ одной парой электродов ПЭП;
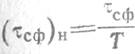 —нормированная
к номинальному периоду решетки ПЭП длительность импульсной
характеристики СФ.
—нормированная
к номинальному периоду решетки ПЭП длительность импульсной
характеристики СФ.
Такая зависимость амплитуды выходного импульса от времени объясняется (линейностью ее возрастания при 'распространении ПАВ вдоль эквидистантной решетки ПЭП (рис. 3.3,д).
При наличии нестабильности длительности ![]()
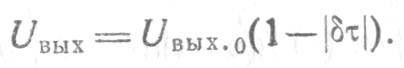
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.