Рассмотрим связь аналогового сигнала с соответствующим ему цифровым кодом.
2.6.2. Связь между аналоговыми и дискретными сигналами
Согласно теореме
Котельникова аналоговый сигнал с ограниченным спектром U (t) может быть точно (без потери информации) преобразован в
дискретный сигнал U(n![]() )
и затем точно восстановлен по отсчетам этого дискретного сигнала.
Практически любой аналоговый сигнал имеет ограниченный спектр и поэтому может
быть заменен при правильно выбранной частоте дискретизации соответствующим
дискретным сигналом.
)
и затем точно восстановлен по отсчетам этого дискретного сигнала.
Практически любой аналоговый сигнал имеет ограниченный спектр и поэтому может
быть заменен при правильно выбранной частоте дискретизации соответствующим
дискретным сигналом.
Исследуем вопрос о тех
преобразованиях спектра, которые наблюдаются при дискретизации произвольного
аналогового сигнала. Для этого обратимся к формуле (2ю2) и заметим, что дискретный
сигнал U(n![]() )
является произведением аналогового сигнала U(t) и так называемой дискретизирующей последовательности
)
является произведением аналогового сигнала U(t) и так называемой дискретизирующей последовательности
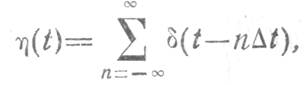
образованной 8-импульсами,
которые следуют через равные интервалы времени ![]() . Как известно, спектр произведения
двух сигналов выражается через свертку их спектральных плотностей. Поэтому,
если известны законы соответствия сигналов и спектров:
. Как известно, спектр произведения
двух сигналов выражается через свертку их спектральных плотностей. Поэтому,
если известны законы соответствия сигналов и спектров: ![]() , то спектральная плотность дискретного сигнала U(n
, то спектральная плотность дискретного сигнала U(n![]() ) будет равна
) будет равна
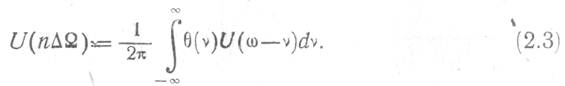
Для нахождения
спектральной плотности ![]() разложим периодическую
функцию
разложим периодическую
функцию ![]() в ряд Фурье:
в ряд Фурье:

Коэффициенты этого ряда
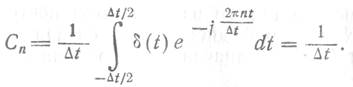
Если вынести 1/![]() из под знака
из под знака ![]() выражения
(2.4) и реализовать преобразование Фурье, то
выражения
(2.4) и реализовать преобразование Фурье, то ![]() будет равно
будет равно
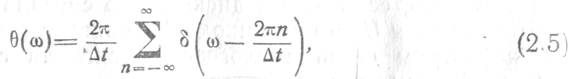
т. е. спектр
дискретизирующей последовательности состоит из бесконечной совокупности ![]() -импульсов в частотной
области, располагающихся через одинаковые
промежутки
-импульсов в частотной
области, располагающихся через одинаковые
промежутки ![]() .
.
Подставляя (2.5) в (2.3) и изменяя порядок следования операций суммирования и интегрироващия, находим
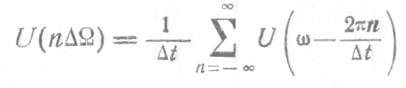
или
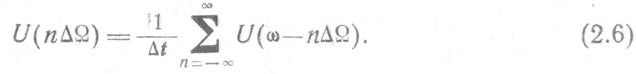
Таким образом, спектр
дискретного сигнала представляет собой (с точностью до масштабного множителя ![]() ) результат, суммирования
бесконечного числа «копий» спектра аналогового сигнала. Эти копии
располагаются на оси частот через равные промежутки частот
) результат, суммирования
бесконечного числа «копий» спектра аналогового сигнала. Эти копии
располагаются на оси частот через равные промежутки частот ![]() .
.
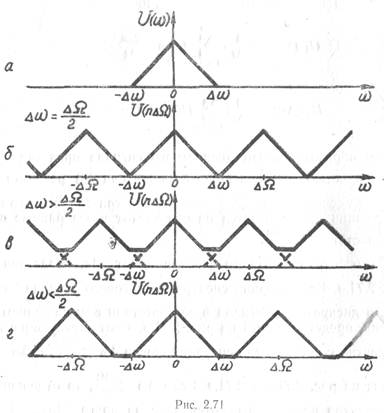
Пусть спектр аналогового
сигнала имеет вид, представленный на рис. 2.71,а. Если ширина спектра
аналогового сигнала ![]() , то спектр дискретного сигнала в
соответствии с выражением (2.6) имеет вид, представленный на рис. 2.71,6.
Соответствующие спектры дискретного сигнала для ситуации, когда
, то спектр дискретного сигнала в
соответствии с выражением (2.6) имеет вид, представленный на рис. 2.71,6.
Соответствующие спектры дискретного сигнала для ситуации, когда ![]() , показаны на рис. 2.71,2 и
2.71,в. Если
, показаны на рис. 2.71,2 и
2.71,в. Если ![]() , то
отдельные лепестки спектра не накладываются друг на друга. Поэтому такой
аналоговый сигнал может быть вновь восстановлен с помощью фильтра низкой
частоты (ФНЧ). Наибольшее допустимое значение шага дискретизации составит при
этом
, то
отдельные лепестки спектра не накладываются друг на друга. Поэтому такой
аналоговый сигнал может быть вновь восстановлен с помощью фильтра низкой
частоты (ФНЧ). Наибольшее допустимое значение шага дискретизации составит при
этом ![]() , что
полностью согласуется с теоремой Котельникова.
, что
полностью согласуется с теоремой Котельникова.
Идеальный ФНЧ, служащий для восстановления аналогового сигнала, должен иметь частотный коэффициент передачи
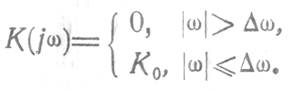
Однако такой ФНЧ физически
нереализуем. Реальный ФНЧ имеет амплитудно-частотную характеристику, которая
охватывает один или несколько лепестков спектра дискретного сигнала. Это
приведет к искажению спектра исходного сигнала. Для уменьшения этого эффекта
обычно выбирают ![]() ,
т. е.
,
т. е. ![]() . Это условие
несколько снижает требования к АЧХ ФНЧ и позволяет реализовать их на основе
цифровых фильтров типа Чебышева или Баттерворта [13].
. Это условие
несколько снижает требования к АЧХ ФНЧ и позволяет реализовать их на основе
цифровых фильтров типа Чебышева или Баттерворта [13].
2.6.3. Погрешности квантования при аналого-цифровом преобразовании
На выходы АЦП с ФД (рис-
2.67) поступают аналоговые напряжения, которые изменяются В соответствии с
динамическим диапазоном УПЧ по выходу. Эти сигналы дискретизируются, квантуются
и переводятся в цифровые коды. На выходе преобразователя сигнал представляется
в формате с фиксированный запятой. Шаг квантования ![]() , определяющий точность преобразования,
задается разрядностью преобразователя L (т. е. длиной его слова). Максимальное количество различных
чисел, представленных с помощью двоичного кода разрядности L, равно
, определяющий точность преобразования,
задается разрядностью преобразователя L (т. е. длиной его слова). Максимальное количество различных
чисел, представленных с помощью двоичного кода разрядности L, равно
![]()
Отсюда для знакопеременного сигнала можно найти шаг квантования:
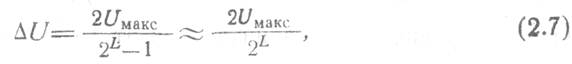
где UMакс — максимальный уровень напряжения на входе АЦП.
Соотношения между разрядностью АЦП и величиной шага квантования проиллюстрируем примером.
Пример 1.
Для АЦП типа 1107 ПВ2 максимальное значение знакопеременного напряжения составляет 1В, при длине слова в 8 двоичных разрядов. Тогда шаг квантования равен
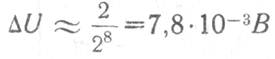
Амплитудный квантователь, как видно из его амплитудной характеристики (см. рис. 2.78), является нелинейным элементом. Квантование приводит к искажению дискретного сигнала, которое называется шумами квантования. На практике часто АК представляют четырехполюсником, а выходное напряжение записывают как сумму истинного значения входного напряжения и отсчета шума квантования, т. е.
![]()
Учтем, что входной сигнал
АЦП имеет полезную и шумовую составляющие. Последняя обусловлена внутренними
шумами приемного устройства и представляет собой стационарный белый гауссовый
шум с известным распределением ![]() . Тогда (2.й) приводится к виду
. Тогда (2.й) приводится к виду
![]()
Если считать, что шум квантования представляет собой случайный процесс, некоррелированный с сигналом и шумом приемника, то АК можно рассматривать как второй источник шума, обусловленного только квантованием. В литературе показано, что шум квантования имеет следующие статистические характеристики:
1) Математическое ожидание шума квантования
![]()
2) Дисперсия шума квантования

 т. е. она равна одной двенадцатой квадрата разности между дискретными
уровнями. Нетрудно заметить, что дисперсия шумов квантования совпадает с
дисперсией случайной величины, распределенной равномерно на интервале от
т. е. она равна одной двенадцатой квадрата разности между дискретными
уровнями. Нетрудно заметить, что дисперсия шумов квантования совпадает с
дисперсией случайной величины, распределенной равномерно на интервале от ![]() до
до ![]() . Это происходит потому,
что при малой величине разности между дискретными уровнями погрешность
квантования достаточно точно аппроксимируется отрезками прямых линий (за
исключением тех случаев, когда сигнал между дискретными уровнями проходит через
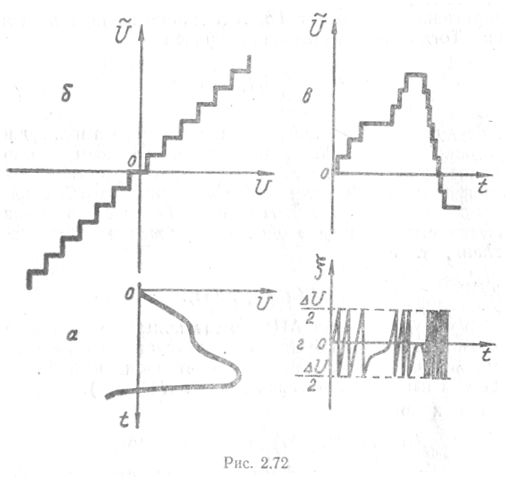
экстремум). Процесс квантования сигнала по амплитуде иллюстрируется рис.
2.72. С целью упрощения рисунка на нем не
. Это происходит потому,
что при малой величине разности между дискретными уровнями погрешность
квантования достаточно точно аппроксимируется отрезками прямых линий (за
исключением тех случаев, когда сигнал между дискретными уровнями проходит через
экстремум). Процесс квантования сигнала по амплитуде иллюстрируется рис.
2.72. С целью упрощения рисунка на нем не
показана дискретизация
сигнала. Из рисунка видно, что шумы квантования распределены равномерно в
интервале от ![]() до
до
![]() (рис 2.73).
(рис 2.73).
3) Ширина энергетического спектра шумов квантования существенно шире ширины спектра исходного квантуемого сигнала
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.