Знак гармонической импульсной
характеристики путем замены суммирующего устройства на вычитающее. Для фильтрации
во всем диапазоне доплеровских частот применяют набор резистивных матриц ![]() ,
, ![]() .
.
Инверторы, установленные перед одним из входов сумматоров для мнимых составляющих корреляционной суммы, необходимы для учета комплексной сопряженности характеристики (3.27)
Схема рис. 3.22 может быть использована и для согласованной фильтрации КФМ радиоимпульсов. Для этого необходимо в соответствии с кодом этого сигнала использовать не только прямые, но и инверсные выходы триггеров в разрядах регистров сдвига.
В заключение отметим, что применение бинарного квантования/как и жесткого амплитудного ограничителя, дает дополнительные потери в отношении сигнал-шум порядка 2 дБ [10], а переход к аналого-цифровой схеме (рис. 3.22) резко снижает стабильность характеристик фильтра. Поэтому цифровую согласованную фильтрацию сигналов с большой базой часто производят с помощью согласованного фильтра в частотной области (рис. 3.13). Особенностью цифровой технической реализации данной схемы является вычисление прямого и обратного дискретных преобразований Фурье (3.32), а также использование цифровой схемы матричного умножителя, например типа рис. 3.20.
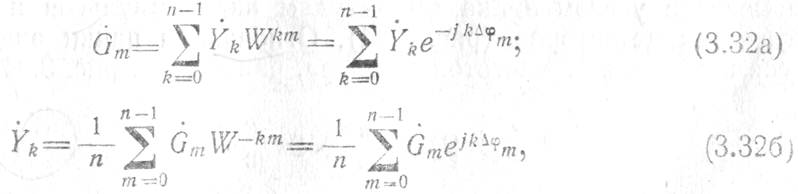
где
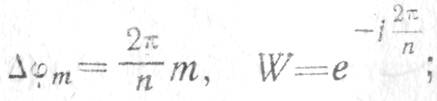
k,
m=0,l,2,...n — номера
временной выборки комплексной амплитуды ![]() принимаемого
сигнала и частотной выборки ее спектра
принимаемого
сигнала и частотной выборки ее спектра ![]() соответственно;
соответственно;
п — число временных либо частотных выборок, участвующих в преобразовании Фурье.
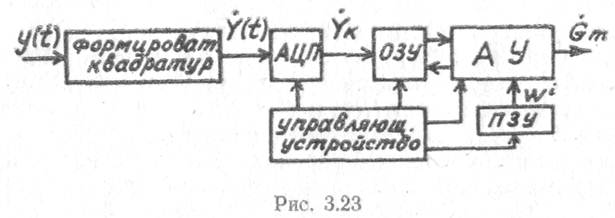
Ввиду схожести алгоритмов 3.32а и 3.326 на практике они реализуются, как правило, в одном и том же вычислителе (процессоре) ДПФ (рис. 3.23)
Рассмотрим в качестве примера вычисление прямого ДПФ когерентной пачки простых прямоугольных радиоимпульсов, отраженных от движущейся цели. Напомним, что при цифровой обработке сигналов в двух квадратурных подканалах интервалы временной и частотной дискретизации определяются выражениями соответствено

где ![]() —
разрешающие способности по времени запаздывания и частоте соответственно. Для
упрощения анализа будем полагать, что
—
разрешающие способности по времени запаздывания и частоте соответственно. Для
упрощения анализа будем полагать, что ![]() , т. е. за длительность импульса укладывается
лишь одна временная выборка. Данные условия означают, что значения цифровых
кодов на выходах АЦП будут пропорциональны с учетом знака амплитудам
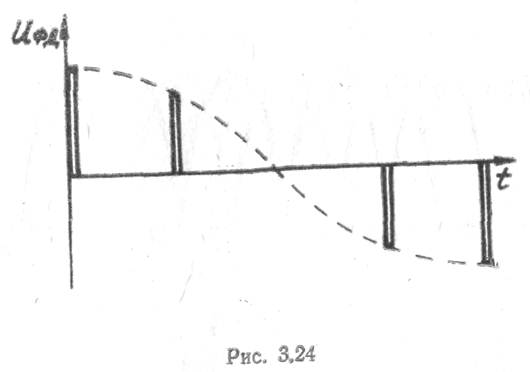
видеоимпульсов на выходах фазовых детекторов (рис. 3.24). Огибающая пачки
видеоимпульсов изменяется с частотой Доплера, равной для рис. 3.24
, т. е. за длительность импульса укладывается
лишь одна временная выборка. Данные условия означают, что значения цифровых
кодов на выходах АЦП будут пропорциональны с учетом знака амплитудам
видеоимпульсов на выходах фазовых детекторов (рис. 3.24). Огибающая пачки
видеоимпульсов изменяется с частотой Доплера, равной для рис. 3.24
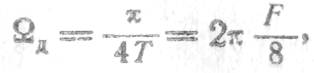
где F — частота повторения импульсов.
Покажем, что вычисление «-той частотной
выборки Gт (3.32а) в дискретном спектре пачки видеоимпульсов
эквивалентно определению выходного напряжения доплеровского фильтра с резонансной
частотой ![]() . Для
этого сумму в правой части выражения (3.32а) запишем как дискретное
представление интеграла Дюамеля, т. е. как выходное напряжение фильтра
. Для
этого сумму в правой части выражения (3.32а) запишем как дискретное
представление интеграла Дюамеля, т. е. как выходное напряжение фильтра
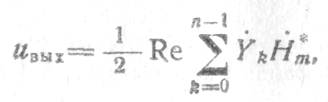
где 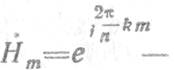 комплексная импульсная характеристика
узкополосного фильтра с резонансной частотой
комплексная импульсная характеристика
узкополосного фильтра с резонансной частотой 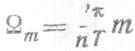 .
.
Действительно, после умножения и деления показателя степени
у Нт на T получаем Нт=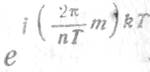 . Так как Н„
имеют прямоугольные огибающие, то АЧХ эквивалентных линейных фильтров
. Так как Н„
имеют прямоугольные огибающие, то АЧХ эквивалентных линейных фильтров
имеют огибающие вида sinx/x с одинаковыми
коэффициентами передачи на своих резонансных частотах ![]() , а полосы пропускания этих фильтров на уровне 0,64 обратно
пропорциональны длительности их импульсных характеристик, т. е.
, а полосы пропускания этих фильтров на уровне 0,64 обратно
пропорциональны длительности их импульсных характеристик, т. е. ![]() . Таким образом, АЧХ
эквивалентных линейных фильтров, напряжения на выходе которых равняются
амплитудам частотных выборок ДПФ, являются взаимно ортогональными (рис.
3,25,а только главные
. Таким образом, АЧХ
эквивалентных линейных фильтров, напряжения на выходе которых равняются
амплитудам частотных выборок ДПФ, являются взаимно ортогональными (рис.
3,25,а только главные
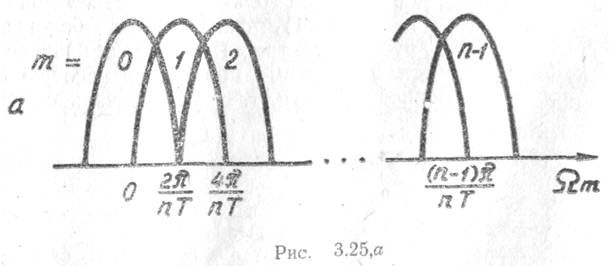
лепестки АЧХ). Выражение для комплексного коэффициента передачи этих фильтров получено в работе [24]:
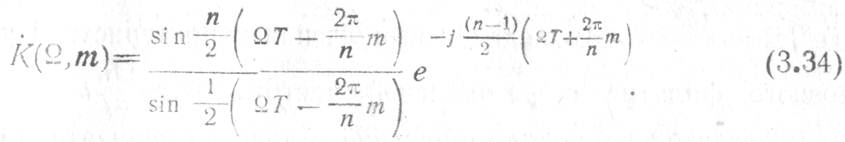
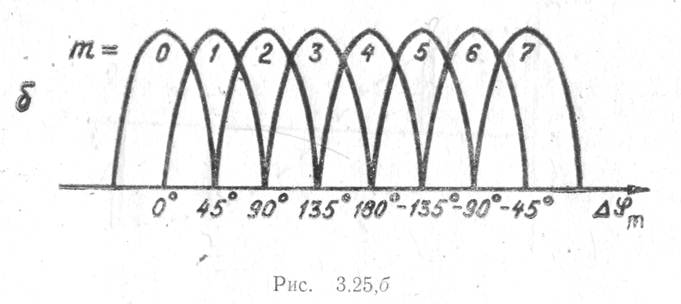
На рис. 3.25,6 в качестве примера для
8-точечного ДПФ (п=8)показаны также амплитудно-фазовые
характеристики (главные лепестки) эквивалентных фильтров, т. е. зависимости
их коэффициента передачи от фазового сдвига ![]() , с которым суммируются временные выборки.
, с которым суммируются временные выборки.
В ряде случаев вышеописанный процесс вычисления ДПФ, называемый цифровым спектральным анализом, имеет самостоятельное значение, например, в системах СДЦ, когда вычисленные значения частотных выборок Gm поступают не на умножитель (рис. 3.13), а (после некогерентного накопления) на пороговое устройство. Из рис. 3.25 следует, что только в один эквивалентный частотный фильтр попадают лишь сигналы, имеющие от выборки к выборке фазовый сдвиг, кратный 2π/п. Для примера рис. 3.24 это означает, что ввиду низкой частотной избирательности фильтров (АЧХ вида sinx/x) сигналы, отраженные от малоскоростных целей и пассивных помех, попадают не только в «нулевой» доплеровский фильтр, но также в 1-й и (n—1)-й фильтры, а по боковым лепесткам АЧХ и во все другие фильтры. Поэтому для повышения частотной избирательности необходимо произвести весовую обработку выборок во временной области, т. е. реализовать «взвешенное» ДПФ
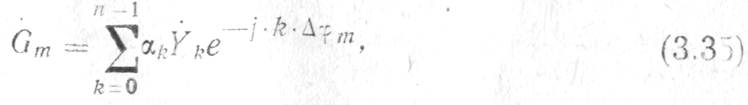
где 0<![]() < 1 —весовые коэффициенты.
< 1 —весовые коэффициенты.
Весовые коэффициенты ![]() обеспечивают формирование симметричной
функции, необходимой для получения высокоизбирательных частотных характеристик
эквивалентных фильтров, описываемых, например, функцией Чебышева или
Баттерворта. Такую функцию со спадающими к краям значениями в литературе часто
называют временным «окном». В зависимости от требований к разрешающей
способности по частоте, уровню боковых лепестков АЧХ, ее неравномерности в
полосе пропускания и т. д. находят применение различные «оконные» функции —
треугольные, гауссовы, Хемминга и др. [И], но наиболее широкое распространение
получили косинусоидальные распределения
обеспечивают формирование симметричной
функции, необходимой для получения высокоизбирательных частотных характеристик
эквивалентных фильтров, описываемых, например, функцией Чебышева или
Баттерворта. Такую функцию со спадающими к краям значениями в литературе часто
называют временным «окном». В зависимости от требований к разрешающей
способности по частоте, уровню боковых лепестков АЧХ, ее неравномерности в
полосе пропускания и т. д. находят применение различные «оконные» функции —
треугольные, гауссовы, Хемминга и др. [И], но наиболее широкое распространение
получили косинусоидальные распределения ![]() , например, вида
, например, вида
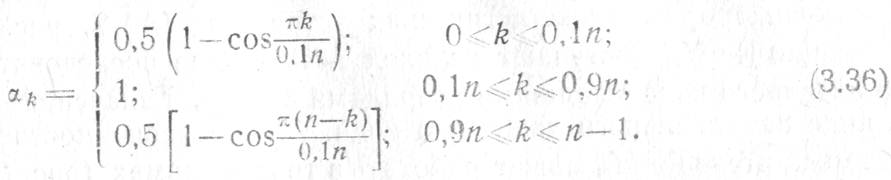
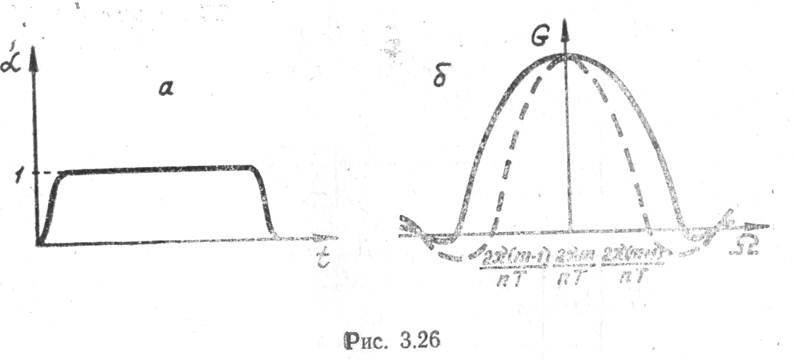
Достоинством данной «оконной» функции является
то, что 80% временных отсчетов ![]() в середине интервала
в середине интервала ![]() не требуют умножения на
не требуют умножения на ![]() . На рис. 3.26,а, б представлена
функция
. На рис. 3.26,а, б представлена
функция ![]() (3.36) и
соответствующая ей нормированная АЧХ эквивалентного фильтра
(3.36) и
соответствующая ей нормированная АЧХ эквивалентного фильтра
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.