Приемно-передающие устройства радио­технических систем: Учебное пособие, страница 28

По величине напряжения на выходе ФД можно судить об откло­нении фазы сигнального напряжения относительно фазы опорного напряжения.

Качество работы ФД определяется детекторной характеристи­кой, представляющей собой зависимость выходного напряжения от разности  фаз  подаваемых  на  вход  напряжений   .

Основными параметрами ФД являются крутизна амплитудно-фазовой характеристики  и входное сопротивление -

Под крутизной амплитудно-фазовой характеристики понимает­ся производная от выходного напряжения  по разности фаз входных   напряжений   :

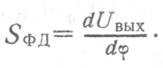
Под входным сопротивлением понимается отношение амплиту­ды подводимого гармонического напряжения к амплитуде первой гармоники   входного   'тока,.

По устройству л принципу действия ФД аналогичны преобра­зователям частоты- Различие состоит лишь в том, что на вход ФД воздействуют сигнальное и опорное напряжения, совпадаю­щие по частоте. Поэтому величина выходного напряжения зависит от разности фаз входных напряжений. Чтобы выделить это напря­жение, в качестве нагрузки применяют не резонансный фильтр, как в преобразователях частоты, а фильтр низкой частоты типа RC. В принципе все схемы преобразователей частоты можно ис­пользовать в качестве ФД, заменив в них гетеродинное напряже­ние на опорное, а фильтр промежуточной частоты—на низкочас­тотный фильтр RC. Наиболее широкое применение находят ба­лансные   фазовые   детекторы.

Принципиальная схема балансного ФД представлена на рис. 2.57. Он состоит из двух амплитудных диодных детекторов, включенных по балансной схеме, на входы которых с помощью резонансных трансформаторов приложены сигнальное U_c и опор­ное U₀ напряжения. При этом одно из напряжений, например си­гнальное, действует на первый

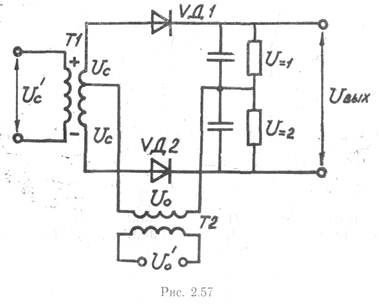
и второй амплитудные детекторы в противофазе, а другое — опорное, приложено синфазно (рис. 2.57).

Найдем аналитическое выражение для амплитудно-фазовой характеристики. В соответствии с рис. 2.57 к диоду УД1 приложе­но   напряжение

к диоду УД2 — напряжение

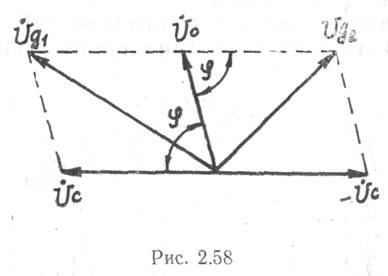
Для определения амплитуд этих напряжений  и  пост роим векторную диаграмму (рис. 2.58). В соответствии с обозна­чениями,   принятыми   на   рисунке,

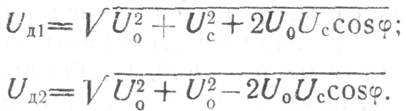
С учетом этого напряжение на выходе ФД (рис. 2.58) опреде­ляется   равенством

Подставив в эту формулу выражения  ,    и обозначив  через т, получим

На практике возможны два случая: . В случае, когда ,   выражение  преобразуется к виду

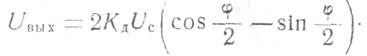
В случае, когда , справедливо следующее приближенное выражение:

Амплитудно-фазовые   характеристики   графически   представле­ны на   рис.   2,59.

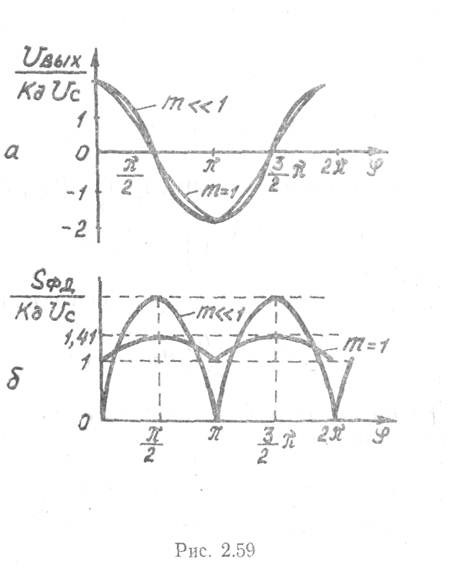
Крутизна   амплитудно-фазовой   характеристики   определяется следующими   выражениями: для   случая   т = 1

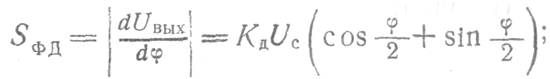
для случая

Зависимости крутизны амплитудно-фазовой характеристики от разности фаз представлены на рис. 2.59,б. В случае т = 1 амплитудно-фазовая характеристика отличается повышенной ли­нейностью. Однако максимальная крутизна амплитудно-фазовой характеристики выше при . Поскольку амплитудно-фазовая характеристика переходит через нуль при разности фаз сравни­ваемых   колебаний,  равной   ,   имея   при  этом   максимальную крутизну,  то  исходный  фазовый   сдвиг  сравниваемых   колебании выбирается   равным   .

В  соответствии  с  определением  и   обозначениями,   принятыми на рис. 2.57, входное сопротивление по сигнальному входу

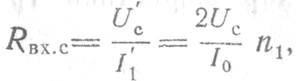
где п₁ — коэффициент трансформации сопротивления  по сигналь­ному   входу.

В   исходной   рабочей   точке      имеем

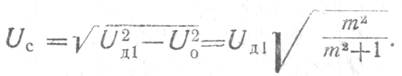
Подставив это выражение в формулу для R_вх, получим

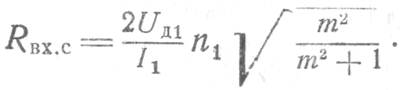
Входное сопротивление по  входу опорного напряжения

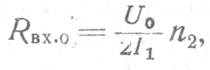
где   п₂ — коэффициент   трансформации   сопротивления   по   входу опорного   напряжения-

2.5.4. Корреляционные детекторы

В приемных трактах современных активных и пассивных ра­диолокаторов широко используется корреляционная обработка сигналов. Из теории обнаружения слабых сигналов следует, что одной из основных операций, выполняемых различными устройст­вами когерентной оптимальной обработки сигналов, является вычисление корреляционных интегралов или их огибающих (мо­дульных   значений)   вида:

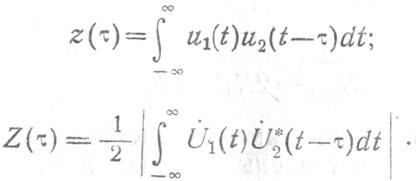
Обрабатываемые высокочастотные напряжения U₁(t) и U₂(t) (U₁(t) и U₂(t)—их комплексные амплитуды) могут быть оба принятыми или принятым и опорным колебаниями. Каждое из них может быть случайным процессом или суммой случайного и детерминированного.процессов. На конечном интервале времени эти случайные процессы можно полагать стационарами эргодическими с нулевыми  средними  и  нормально  распределенными мгновенными значениями. При этом корреляционный интеграл пропорционален взаимно-корреляционной функции напряжений u₁(t) и u₂(t):

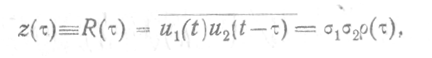
где  -средние  квадратические  значения  входных   напряжений;

 —нормированная   взаимно-корреляционная   функция,   ха-( рактеризующая   степень   связи    (корреляции) между входными колебаниями в зависимости от их взаимного временного сдвига .

Примерами коррелированных процессов могут служить сигна­лы активных, в том числе шумовых, помех от одного источника, принимаемые разнесенными приемниками пассивного радиолока­тора. Коррелированными являются отраженный от цели и зон­дирующий   сигналы   активного   радиолокатора.

Коррелированные сигналы поступают на фоне помех от дру­гих источников и флюктуационных шумов. Эти помехи составляют некоррелированный фон, или просто шум. Поэтому в общем слу­чае входные процессы являются суммой сигнальной (коррелиро­ванной)   и   шумовой    (некоррелированной)   составляющих:

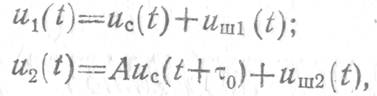
где  -исходный временной сдвиг сигналов, а А –амплитудный множитель.

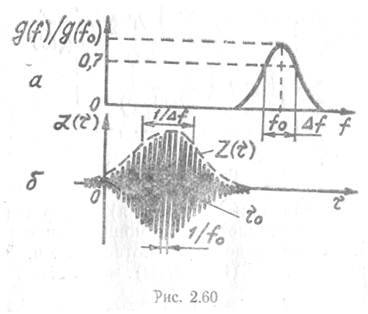
Ширина   спектра   входных   сигналов  ,   как  правило,   много меньше несущей частоты   (рис. 2.60,а). Поэтому их называют «узкополосными». Для таких сигналов , как и , имеет импульсный осциллирующий характер, а огибающая  дости­гает максимума при компенсации взаимного сдвига сигналов:  (рис. 2.60,б).   Коэффициент   взаимной   корреляции

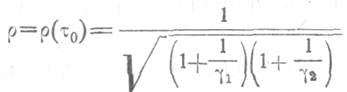
зависит от отношений  и  мощностей (диспер­сий) сигналов и шумов на первом и втором входах. Полные мощ­ности входных процессов характеризуются дисперсиями