Приемно-передающие устройства радио­технических систем: Учебное пособие, страница 45

(рис. 3.26,6 сплошная линия, пунктиром показана исходная АЧХ вида sinxlx). Из данного рисунка следует, что ценой ухуд­шения разрешающей способности по частоте (расширение главно­го максимума АЧХ) применение временного «окна» позволило повысить прямоугольность АЧХ эквивалентных фильтров и сни­зить уровень ее боковых лепестков. Так, например, для времен-* кого «окна», описываемого функцией Кайзера-Бесселя [11], уровень боковых лепестков АЧХ достигает — 82 дБ при расшире­нии ее главного максимума на уровне — 3 дБ примерно в 2 ра­за. Максимальные потери при вычислении взвешенного ДПФ не превышают   3...4 дБ   [12].

Учитывая эквивалентность операций умножения функций во временной области свертке спектров этих функций в частотной области, весовую обработку можно также реализовать взвешен­ным суммированием соседних спектральных отсчетов на выходе вычислителя ДПФ (частотное «окно»). Значения весовых коэф­фициентов   как для временного, так и для частотного «окна» представляются  с  высокой     точностью в  виде  многоразрядного двоичного   кода.

Структурная схема устройства взвешенного ДПФ (3.35) для одной частотной выборки может быть представлена в виде рис. 3.19, где  Операции умножения на  могут производиться не только в МУ (рис. 3.20), но и при наличии вре­мени (например, в случае доплеровской фильтрации — рис. 3.24) с помощью арифметико-логических устройств (АЛУ, рис. ^.27). Значения Re поступают на вход АЛУ в виде последовательно­го двоичного кода младшими разрядами вперед, а значения Re в виде параллельного двоичного кода. АЛУ в зависимости от ко­да множителя Re может работать в трех режимах (рис. 3.27,6). Учитывая, что , целесообразно разрядность представле­ния произведения ограничить равной разрядности множимого ,

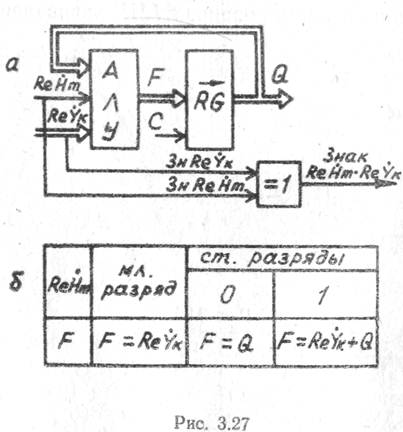
отбрасывая в регистре младшие разряды путем подачи на него импульсов сдвига С после образования каждой промежуточной суммы. Знак произведения определяется с помощью схемы «ис­ключающее   ИЛИ».

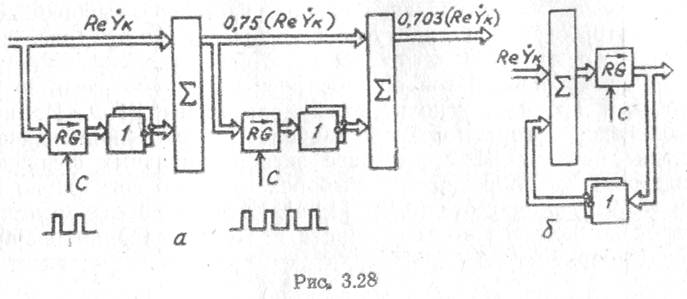
Другим способом последовательно-параллельного умножения может быть схема, реализующая итерационный алгоритм (рис.   3.28).

В состав схемы (рис. 3.28,а) входят ряд последовательно включенных комбинационных сумматоров, осуществляющих сум­мирование прямого кода 1-го слагаемого с обратным кодом част­ного от деления 1-го слагаемого на 2^l, где l — число импульсов сдвига на регистрах, установленных на вторых входах сумматоров. При необходимости получения высокой точности вычисления множителя схема получается громоздкой, поэтому ее часто заме­няют   схемой рис.   3.28,6.

Рассмотрим требования, предъявляемые к блокам вычислителя ДПФ  (рис, 3.23), Объем памяти входных ОЗУ    оценивается по формуле

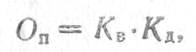
где  — количество выборок с одной дальности;

—количество   дискрет   дальности.

В случае, когда =п (числу точек ДПФ), последняя форму­ла   принимает   вид

где —максимальное  время     задержки     обнаруживаемого

сигнала;

— требуемые разрешающие способности цифрового приемного устройства по частоте и времени запаздывания соот­ветственно;

 — коэффициент, учитывающий расширение полосы пропус­кания эквивалентного фильтра-ДПФ за счет весовой обработки входной последовательности во временном «окне», например, для   функции    (3.36)    =1,21.

Число разрядов представления чисел п_р определяется динами­ческим диапазоном изменения входных сигналов плюс знаковый разряд

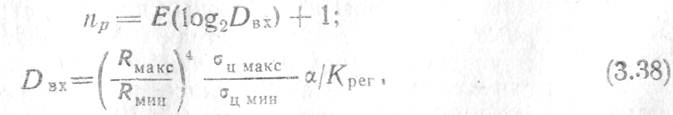
где дБ — коэффициент, учитывающий флуктуации ампли­туды сигнала за счет изменения условий распространения радио­волн;

K_per — коэффициент   регулирования   системы   АРУ.

Учитывая реальные значения D_вх  100 дБ для радиолока­ционных приемников, а также значения радиолока­ционных сигналов в соотношении (3.28), справедливом и для ДПФ, делаем вывод, что вычисление каждой частотной выборки ДПФможет потребовать миллиардного быстродействия АУ (рис. 3.23), работающего в 16-разрядной сетке. Поэтому в случае приема сигналов с большой базой при построении ЦСФ в частотной об­ласти, как правило, используются алгоритмы БПФ. Из всего многообразия алгоритмов БПФ наиболее широкое применение на практике находит БПФ в базисе экспоненциальных функций с использованием прореживания выборок входного сигнала по вре­мени (3.39) и по частоте (3.40) [1,20]. Если число «n» временных выборок не является степенью числа 2, то оно дополняется нуле­выми   выборками

где m=0,1,2,…, n;

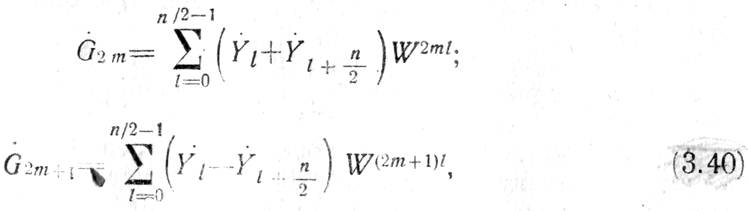
где т=0, 1, 2.....п 2—1.

В качестве примера на рис. 3.29,а и б представлены направ­ленные графы вычисления 8-точечного БПФ для алгоритмов с прореживанием по времени и по частоте соответственно. Кружка­ми обозначены сумматоры комплексных чисел, а стрелками вдоль соединительных линий — умножители комплексных чисел на множитель,   указанный   возле   стрелки.

Общая структурная схема вычислителя (процессора) БПФ сох­раняется такой же, как и у вычислителя ДПФ (рис. 3.23), однако построение его  АУ значительно     упрощается  ввиду уменьшения необходимого числа умножителей комплексных чисел в 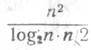   раз  [1]. Так как на всех этапах БПФ   (рис. 3.29,а, б)  выполня­ется одна и та же базовая операция, то структурные схемы АУ в

обоих случаях могут содержать лишь один базовый процессор (БП), последовательно реализующий временную (рис. 3.30.а) либо частотную  (рис. 3.30,6)  «бабочку» Адамара.

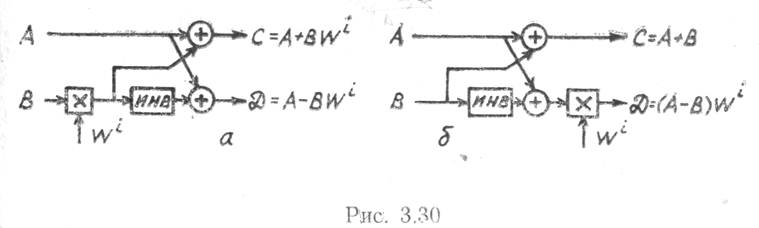
Входными операндами такого про­цессора являются комплексные числа, соответствующие квадра­турным составляющим выборок входного сигнала или результа­там, полученным на каждом из этапов БПФ. Эти результаты по­мещаются, как правило, в освобождающиеся ячейки входного ОЗУ. В соответствии с рис. 3.30 БП БПФ может быть реализован на сумматорах многоразрядных кодов с параллельным переносом, инверторах на  логических элементах и матричных умножителях.