Задача заключается в том, чтобы найти удобные соотношения, позволяющие применить к анализу каскадов, содержащих нелинейные элементы, уже известную общую теорию шумящего четырехполюсника с постоянными параметрами.
Физические свойства нелинейного элемента определяют вид его характеристики. У резистивного элемента вольтамперная характеристика может быть линейно-ломанной, квадратичной и экспоненциальной. При этом для резистивного элемента сохраняется зависимость
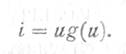
Если элемент емкостной, то в зависимости от его свойств меняется вид вольтфарадной характеристики, выражающей зависимость емкости от напряжения. Для нелинейного конденсатора всегда сохраняются соотношения
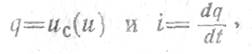
где q — заряд электрона.
В случае нелинейной индуктивности свойства цепи определяют вид зависимости потокосцепления от тока Ф =ξ(i) и для нее справедливо равенство Ф = iL(i).
Очень важно то, что во всех случаях оказывается возможным, прикладывая к нелинейному элементу гармоническое переменное напряжение, получить периодическое изменение основного пара-
метра этого элемента (R, С или L) и, таким образом, получить элемент с переменным параметром.
Поскольку «ременная функция является периодической, то ее можно представить в виде ряда Фурье. Если на нелинейный элемент с вольтамперной характеристикой (рис. 1.12) подается напряжениегенератора
где 
то, определив по
вольтамперной характеристике элемента i=f(u) его дифференциальную проводимость g—f(u) можно построить график изменения проводимости во времени g(t) (рис. 1.12).
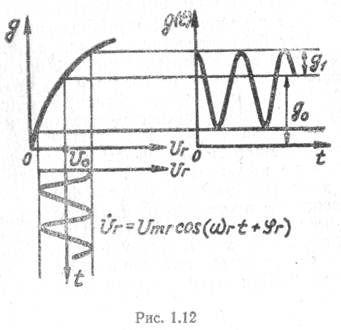
Полученная функция представляется в виде ряда Фурье
,
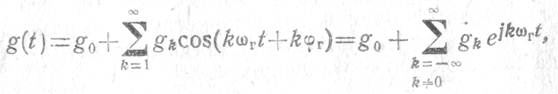где
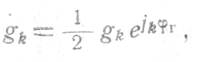
a gk — коэффициент k-того члена ряда Фурье для функции g. Эти коэффициенты находятся для каждого конкретного случая по общей методике.
Аналогично для случая нелинейности емкости C(t) будем иметь
,
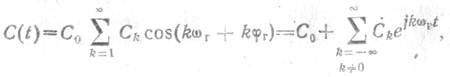где
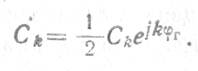
Отметим, что gk и Сk для всех k, кроме k=0, являются комплексными амплитудами k-тых гармоник изменения параметров g и С, a go и Со — постоянными составляющими этих параметров.
Рассмотрим резонансную электрическую цепь, содержащую элементы с переменными параметрами, и установим условия, при которых эта цепь удовлетворяет требованиям линейности.
Цепь (рис. 1.13) содержит входной контур, настроенный на частоту ωс. К контуру приложено напряжение
,
где
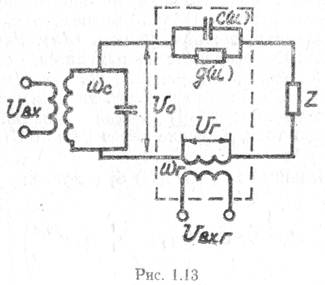
На выходе цепи включена нагрузка Z, в общем случае представляющая собой один или несколько колебательных контуров, настроенных на частоты, отличные от ωс иkωг. - Связь входного контура с нагрузкой осуществляется через нелинейные проводимости g(u) и емкость С (и).
В рассматриваемую цепь с помощью индуктивной связи от отдельного генератора (гетеродина) подано напряжение
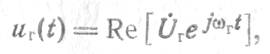
Управляющее параметрами нелинейных элементов. Таким образом, элементы связи g(u) и С (и) под воздействием напряжения генератора становятся элементами с переменными параметрами g (t) и C(t).
Задача сводится к нахождению соотношений между токами и напряжениями в данной цепи в установившемся режиме.
При этом предполагается, что выполняется ряд условий, реализуемых практически.
1. Амплитуда напряжения генератора значительно больше амплитуды напряжения Uc. Это условие дает нам право пренебречь изменением параметров нелинейных элементов под воздействием напряжения сигнала.
2. Все реактивные элементы цепи имеют пренебрежимо малые потери, и добротность колебательных контуров настолько велика, что они являются короткими замыканиями для токов всех частот, хроме области частот, близких к резонансным.
3. В пределах рассматриваемой полосы частот параметры всех элементов (g, С, L) от -частоты не зависят.
4. Между частотами ωс
и ωг, нет дробно-рациональной связи, т. е.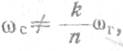 
где k и п — любые целые числа. (Последнее условие не
является обязательным, но оно упрощает анализ).
Для общности можно было рассмотреть в качестве элемент связи также нелинейную индуктивность L(u). Учитывая, что при этом окончательный результат не изменится, ограничимся рассмотрением цепи связи, содержащей только g(u) и С (и). Найдем ток, текущий в данной цепи через элементы связи при коротком замыкании на выходе. Применяя принцип суперпозиции, найдем раздельно токи, текущие через g(t) и C(t), а затем просуммируем их.
Ток через активный элемент g(t) будет равен
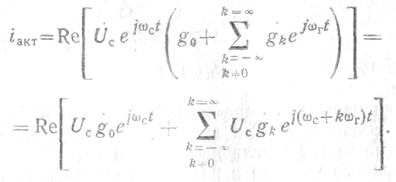
Соответственно, для реактивной составляющей тока через элемент С (t)
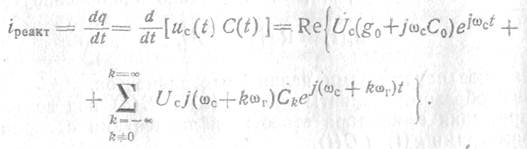
Суммируя эти токи, получим
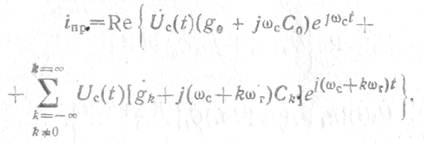
Из полученных соотношений можно сделать следующие доводы:
в составе тока, текущего через элементы связи с переменными параметрами g(t) и C(t), имеются составляющая с частотой , а также комбинационные составляющие с частотами ωк = =kωг+ωo и ωк =kωг - ωo , где k может принимать любые знания от — ∞ до ∞, кроме k=0;
амплитуды всех составляющих тока линейно зависят от амплитуды входного напряжения Uе (поскольку g(t) и C(t) от ic(t) не зависят).
На основании линейной зависимости амплитуд составляющих рока от входного напряжения Uс(t) можно для каждой пары выбранных комбинационных частот представить элементы связи в виде эквивалентного линейного четырехполюсника (рис. 1.14).
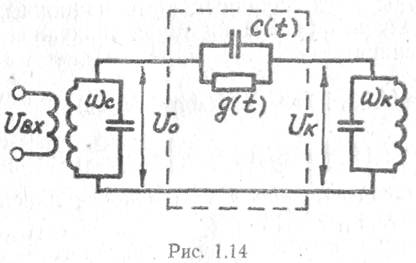
При этом считается, что резонансной нагрузкой является колебательный контур, настроенный на одну из комбинационных частот (при фиксированном k) ωк =ωc+kωг
Ток на этой частоте ωс, обусловленный приложенным на частоте напряжением Uс, равен
Этот ток вызывает падение напряжения на активной проводимости контура:
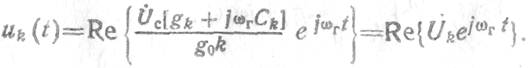
Напряжение uk(t), в свою очередь, окажется приложенным элементам связи, и под его воздействием через них потечет ток iобр
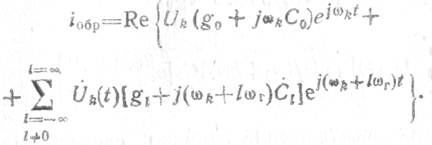
Последнее соотношение можно упростить, если найти связь меж ду индексами суммирования k и l.
Из всей совокупности токов представляют интерес лишь две составляющие на частотах ωс и ωk. Приравнивая частоты ωl =ωk+ lωr, и ωс, ПОЛУЧИМ, ЧТО ωl=ωс + kωr+lωr = ωс только в том случае, если k=—l; l=—k.
Так как
,
то
Если теперь из уравнений для iпр и iобр взять только комплексные амплитуды двух заданных комбинационных частот ωс и ωk, то можно подучить уравнения токов эквивалентного линейного четырехполюсника:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.