Динамический диапазон приемного устройства в значительной степени определяет его помехозащищенность. Большинство существующих способов помехозащиты оказываются эффективными лишь тогда, когда уровень помехи не превышает динамический диапазон.
Чувствительность, избирательность и динамический диапазон приемных систем в значительной мере определяются техническими возможностями элементной базы, на которой они построены.
1.2. Анализ типовых каскадов приемных устройств
1.2.1. Анализ линейных каскадов с постоянными параметрами
К линейным каскадам приемно-передающих систем относятся функциональные элементы, в которых коэффициенты передачи мощности, тока и напряжения не зависят от уровня сигналов, действующих на их входах. При этом по отношению к действующим сигналам выполняется принцип суперпозиции. Это условие называют условием малого сигнала.
Линейные каскады отличаются большим многообразием. Это обусловлено не только использованием различных типов активных усилительных и преобразовательных элементов (электронные, твердотельные, многоэлектродные и т. д.), но и способами включения их основных электродов относительно источника сигнала и нагрузки. Различна реализация входных и межкаскадных цепей усилителей. Эти обстоятельства на определенном этапе развития теории и техники приемно-передающих систем потребовали разработки общей теории, пригодной для анализа и оценки технических параметров линейных каскадов любого типа. Основы такой теории были разработаны советскими учеными, в частности членом-корреспондентом АН СССР В. И. Сифоровым.
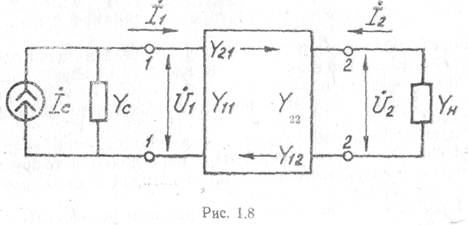
В рамках общей теории линейного усилительного каскада активный усилительный элемент вместе с резонансным контуром на его входе представляется в виде активного шумящего линейного четырехполюсника (рис. 1.8). Четырехполюсник имеет два входных (1-1) и два выходных зажима (2—2). Предполагается, что внутренняя схема четырехполюсника неизвестна, а вся информация о его внутренних параметрах может быть получена по результат измерений комплексных амплитуд токов i1 и i2 и напряжений U1 и U2 на внешних зажимах.
Взаимосвязь между комплексными амплитудами токов и напряжений на внешних зажимах четырехполюсника характеризуется системой двух уравнений:
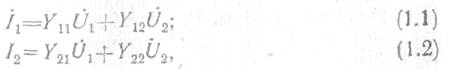
или в матричном виде
![]()
где I,U— векторы токов (i1, i2)T и напряжений (U1 , U2)T; Y— [Yik]— матрица Y-параметров четырехполюсника, которые имеют следующий физический смысл:
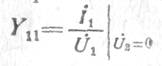 — статическая входная проводимость при коротком замыкании
на выходе;
— статическая входная проводимость при коротком замыкании
на выходе;
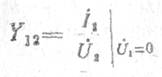 — проводимость обратной передачи при коротком замыкании на входе;
— проводимость обратной передачи при коротком замыкании на входе;
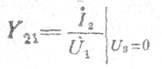 —проводимость (крутизна) прямой передачи при
коротком замыкании на выходе;
—проводимость (крутизна) прямой передачи при
коротком замыкании на выходе;
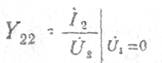 — статическая выходная проводимость при
коротком замыкании на входе.
— статическая выходная проводимость при
коротком замыкании на входе.
Статические Y-параметры (параметры короткого замыкания) не зависят от амплитуд токов и напряжений и неизменны во времени. Их величины определяются свойствами активного усилительного элемента четырехполюсника режимом его работы.
Если Y-параметры четырехполюсника не изменяются во времени, то данный каскад является каскадом с постоянными параметрами. В общем случае все статические проводимости являются комплексными величинами, и их величина зависит от рабочей частоты усилителя:
![]()
gik и bik — активная и реактивная составляющие проводимости соответственно.
При подключении к четырехполюснику источника сигнала и резонансной нагрузки проводимости прямой и обратной передачи Y21 , Y12 определяют вносимые токи на входе и выходе. Поэтому полная эквивалентная схема каскада может быть представлена в виде четырехполюсника, изображенного на рис. 1.9. Так
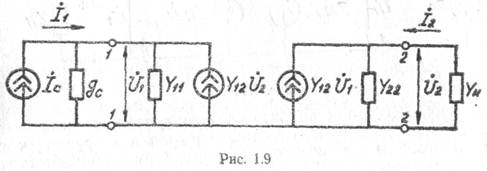
как на выходе четырехполюсника включена нагрузка с комплексной проводимостью YH, то в дополнение к уравнениям (1.1, 1.2) правомерно будет ввести третье уравнение
![]()
Система этих трех уравнений достаточна для определения технических параметров усилительного каскада через Y-параметры. Основное преимущество использования для этой цели параметров короткого замыкания состоит в том, что >на сравнительно низких частотах (до 500 МГц) Y-параметры являются справочными величинами. На более высоких частотах непосредственное измерение параметров короткого замыкания становится затруднительным, и эквивалентные схемы линейных каскадов выражают через внутренние статические Z-параметры или параметры холостого хода.
Уравнения линейного четырехполюсника при этом имеют вид
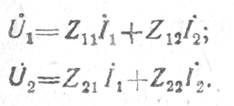
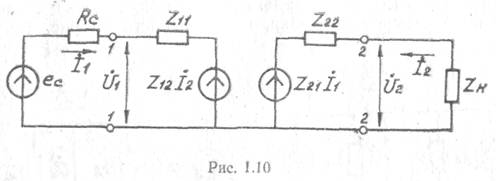
При подключении к четырехполюснику источника сигнала в виде генератора ЭДС с внутренним сопротивлением Rc и резонансной нагрузкой ZН приходят к эквивалентной схеме четырехполюсника, выраженной через Z-параметры (рис. 1.10) -
Полные статические сопротивления прямой и обратной передачи Z21 и Z12 характеризуют вносимые ЭДС на выходе и входе. Очевидно, как и в случае использования системы Y-параметров, при анализе четырехполюсника можно воспользоваться дополнительным уравнением
![]()
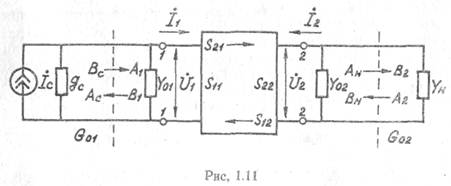
В диапазоне СВЧ при анализе свойств линейных четырехполюсников, подключенных к источнику сигнала и нагрузки через отрезки длинных линий, необходимо учитывать возможность появления отраженных волн из-за рассогласования. Поэтому внутренние параметры активного четырехполюсника целесообразно выражать через коэффициенты матрицы рассеяния, численно равные коэффициентам отражения и устанавливающие связь между падающими и отраженными волнами на входе и выходе четырехполюсника (рис. 1.11).
Уравнения четырехполюсника представляют собой следующую систему уравнений:
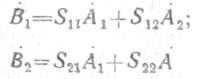 ,
,
или
![]()
где S=[Sik]— матрица рассеяния четырехполюсника, коэффициенты которой имеют следующий смысл;
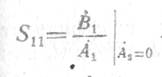 — коэффициент отражения на входе при согласовании
четырехполюсника с нагрузкой;
— коэффициент отражения на входе при согласовании
четырехполюсника с нагрузкой;
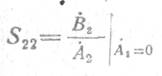 — коэффициент отражения на выходе при согласовании
четырехполюсника с источником сигнала;
— коэффициент отражения на выходе при согласовании
четырехполюсника с источником сигнала;
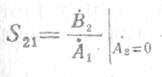 — коэффициент прямой передачи напряжения (тока) в согласованную
нагрузку;
— коэффициент прямой передачи напряжения (тока) в согласованную
нагрузку;
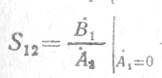 — коэффициент обратной передачи
напряжения А% \Ai=o (тока) при
согласовании на входе.
— коэффициент обратной передачи
напряжения А% \Ai=o (тока) при
согласовании на входе.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.