Для нахождения результирующих шумов вычислений
на выходе ЦСФ воспользуемся методикой, применявшейся для нахождения выходных
шумов амплитудного квантования (3.43, 3.44). Пусть ЦСФ содержит ![]() источников шума вычислений
источников шума вычислений ![]() , а комплексная
характеристика части ЦСФ от
, а комплексная
характеристика части ЦСФ от ![]() -того источника шума до выхода фильтра
равна
-того источника шума до выхода фильтра
равна ![]() . Тогда
дисперсия шумов вычислений на выходе ЦСФ, вызываемых j-тым источником, будет
равна
. Тогда
дисперсия шумов вычислений на выходе ЦСФ, вызываемых j-тым источником, будет
равна
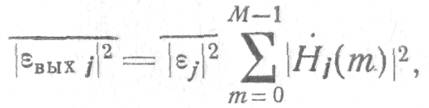
а результирующая дисперсия шумов вычислений на выходе ЦСФ
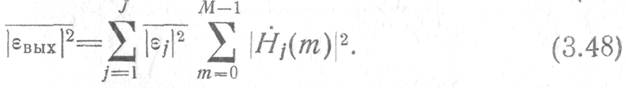
Используя последнее выражение, определим
дисперсию шумов вычислений на выходе ЦСФ (рис. 3.19), вычисляющего либо ДПФ
(считая ![]() ),
либо значение корреляционной суммы во временной области. И в том, и в другом
случае упрощенная структурная схема ЦСФ с учетом ошибок вычислений по одной
),
либо значение корреляционной суммы во временной области. И в том, и в другом
случае упрощенная структурная схема ЦСФ с учетом ошибок вычислений по одной
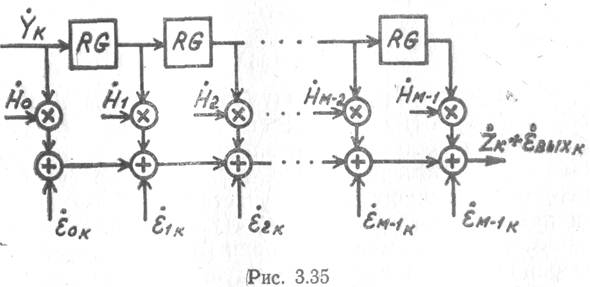
на каждый блок комплексного умножения будет
иметь вид (рис. 3.35). Так как для данной схемы число ошибок равно М, а
все значения ![]() равны
1, то
равны
1, то
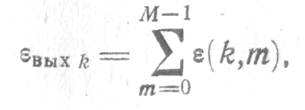
и в соответствии с (3.48) получаем

Необходимо отметить, что для других
структурных схем реализации ЦСФ формула для ![]() приобретает зависимость от
приобретает зависимость от ![]() , т. е. от
параметров фильтра, что позволяет в ряде случаев снизить уровень шумов
вычислений на его выходе [3, 19, 22].
, т. е. от
параметров фильтра, что позволяет в ряде случаев снизить уровень шумов
вычислений на его выходе [3, 19, 22].
Величина шумов вычислений на выходе ЦСФ, реализующих различные алгоритмы БПФ, зависит в общем случае от вида используемого алгоритма. Так как наиболее часто применяются алгоритмы с основанием 2, то определим дисперсию шумов вычислений на выходе такого ЦСФ с прореживанием по времени (результаты анализа при использовании прореживания по частоте остаются примерно те же). С этой целью представим базовую операцию («бабочку») БПФ с учетом аддитивных шумов, возникающих при каждом комплексном умножении на множитель поворота Winв виде рис. 3.36.
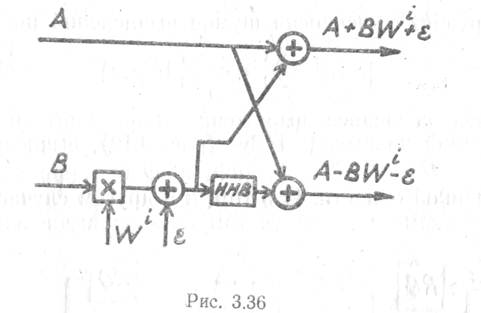
При расчете результирующих шумов вычислений
любой частотной выборки (Gm) БПФ должен быть
учтен вклад каждого из источников шумов, влияющих на значение данной выборки.
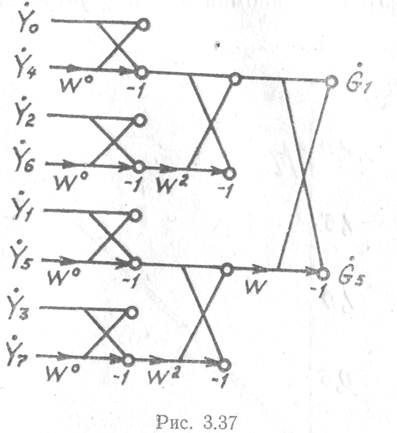
Для этого в качестве примера на рис. 3.37 представлены базовые операции для
8-точечного БПФ, участвующие в формировании первой и пятой частотной выборки.
Из рис. 3.37 следует, что в вычислении каждой частотной выборки БПФ участвует (n—1)-базовая операция. Сохраняя все предыдущие предположения о
статистических характеристиках элементарных источников шума ![]() (к, т), делаем вывод, что
дисперсия результирующих шумов вычисления каждой частотной выборки БПФ
(к, т), делаем вывод, что
дисперсия результирующих шумов вычисления каждой частотной выборки БПФ

Фактически не все базовые операции создают шумы вычислении, так как некоторые (например, на первых двух этапах) включают в себя умножители на единицу. Поэтому выражение (3 50)
необходимо рассматривать как верхнюю границу дисперсии выходного шума вычисления БПФ.
Рассмотрим третий источник собственных шумов
ЦСФ—ошибки за счет квантования значений весовых коэффициентов ![]() фильтра. Такое квантование
обусловлено ограниченностью разрядной сетки запоминающих устройств, в которых
хранятся значения этих коэффициентов. Учитывая большое количество весовых
коэффициентов, эффект их квантования можно заменить эффектом «дрожания», когда
каждый весовой коэффициент заменяется его истинной величиной плюс
последовательность белого шума. Несмотря на приближенность такого анализа, в
среднем величина дисперсии «шума коэффициентов» на выходе ЦСФ оказывается при
этом близка к реальной. Для определения дисперсии «шума коэффициентов»
фильтра. Такое квантование
обусловлено ограниченностью разрядной сетки запоминающих устройств, в которых
хранятся значения этих коэффициентов. Учитывая большое количество весовых
коэффициентов, эффект их квантования можно заменить эффектом «дрожания», когда
каждый весовой коэффициент заменяется его истинной величиной плюс
последовательность белого шума. Несмотря на приближенность такого анализа, в
среднем величина дисперсии «шума коэффициентов» на выходе ЦСФ оказывается при
этом близка к реальной. Для определения дисперсии «шума коэффициентов» ![]() на выходе ЦСФ во временной
области можно воспользоваться выражением (3.48), так как. «шум коэффициентов»
аналогично шуму вычислений зависит от вида структурной схемы ЦСФ.
Подобный анализ может
на выходе ЦСФ во временной
области можно воспользоваться выражением (3.48), так как. «шум коэффициентов»
аналогично шуму вычислений зависит от вида структурной схемы ЦСФ.
Подобный анализ может
быть проведен и при нахождении ![]() на выходе вычислителя БПФ.
на выходе вычислителя БПФ.
В работе [20] показано, что применение данной
методики анализа «шум коэффициентов» дает отношение среднеквадратических
значений шума и сигнала, равное ![]() , где Р—число этапов БПФ;
, где Р—число этапов БПФ; ![]() — цена младшего разряда
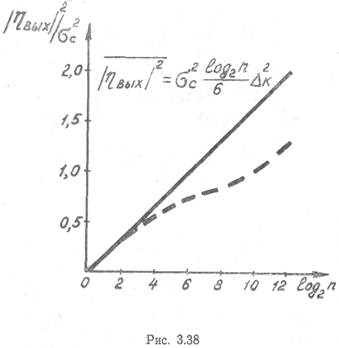
при округлении значений безразмерных весовых коэффициентов. На графике рис.
3.38 представлены расчетное и экспериментальное (пунктир) отношение
— цена младшего разряда
при округлении значений безразмерных весовых коэффициентов. На графике рис.
3.38 представлены расчетное и экспериментальное (пунктир) отношение ![]() как функция количества
этапов БПФ.
как функция количества
этапов БПФ.
Из рис. 3.38 следует, что экспериментальная кривая располагается ниже теоретической на множитель, не превышающий двух, что, по-видимому, связано с точным представлением некоторых 'весовых коэффициентов в запоминающем устройстве вычислителя БПФ.
При использовании представления чисел с фиксированной запятой может -возникнуть дополнительный источник шумов—(колебания (шумы) переполнения разрядной сетки сумматоров ЦСФ, особенно при большом числе временных выборок. Для исключения этих шумов применяют так называемые сумматоры с насыщением [9]. Фиксация переполнения в них достигается путем использования модифицированных кодов, содержащих h дополнительных значений знаковых разрядов, где h=int log2k, а к—число слагаемых. Например, при наличии переполнения в процессе сложения двух чисел (h=1) модифицированный код суммы будет принимать два значения 01 или 10.
Пример: суммирование двух положительных « двух отрицательных чисел при выходе суммы за пределы разрядной сетки (принятая в примере разрядная сетка обеспечивает представление двоичных чисел в пределах от 1.000000= (—64) до 0.111111 = ==(+63))

Модифицированный дополнительный код может быть использован также и при умножении чисел для представления множимого и частичных произведений с целью устранения переполнений при вычислении частичных сумм.
Оценку влияния переполнения на отношение
сигнал-шум ![]() на выходе ЦСФ, учитывая большой уровень вызывающего это
переполнение принимаемого сигнала, обычно не производят. При выполнении условия
на выходе ЦСФ, учитывая большой уровень вызывающего это
переполнение принимаемого сигнала, обычно не производят. При выполнении условия
![]() можно не
учитывать влияние на
можно не
учитывать влияние на ![]() и
шумов временной дискретизации в АЦП, вызванных конечностью интервала
дискретизации
и
шумов временной дискретизации в АЦП, вызванных конечностью интервала
дискретизации ![]() (подразд. 2.6). Если же данное условие не выполняется, то
необходим учет энергетических потерь высокочастотных составляющих спектра
дискретизируемого сигнала, а также, при отсутствии высокоизбирательных
частотных фильтров на входе АЦП, потерь наложения спектров. Такая оценка
произведена в работе [23] для случая цифровой (дискретной) обработки
непрерывного гармонического сигнала с частотой ω на фоне стационарного гауссова
шума n(t) с
экспоненциальной функцией корреляции
(подразд. 2.6). Если же данное условие не выполняется, то
необходим учет энергетических потерь высокочастотных составляющих спектра
дискретизируемого сигнала, а также, при отсутствии высокоизбирательных
частотных фильтров на входе АЦП, потерь наложения спектров. Такая оценка
произведена в работе [23] для случая цифровой (дискретной) обработки
непрерывного гармонического сигнала с частотой ω на фоне стационарного гауссова
шума n(t) с
экспоненциальной функцией корреляции
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.