Приемно-передающие устройства радио­технических систем: Учебное пособие, страница 47

Наиболее быстродействующий матричный процессор БПФ со­держит п/2·log₂n БП БПФ (например, для реализации 8-точеч­ного БПФ на МП серии 1815 требуется 12 БП БПФ, т. е. 48 кор­пусов БИС 1815 ВФЗ). При непрерывной передаче выборок при­нимаемого сигнала на вход такого процессора значения спектраль­ных отсчетов G_m на его выходе будут появляться с периодом, при­мерно равным . Так как значения , как указывалось ранее, в настоящее время составляют ~0,1 мкс, то ширина спектра сиг­налов на входе матричного процессора БПФ, обрабатывающего их в реальном масштабе времени, может составлять единицы МГц.

3.3.1. Шумы цифровой фильтраций

Шумы цифровой фильтрации в значительной степени определяют отношение сигнал-шум на выходе цифрового приемного устройства. Существует три основных независимых источника шумов циф­ровой   фильтрации:

1) шумы   амплитудного квантования   входных   сигналов;

2) шумы, обусловленные неточностью выполнения арифмети­ческих   операций   в   ЦСФ;

3) шумы амплитудного квантования коэффициентов ЦСФ.

Учитывая вышерассмотренные достоинства и недостатки раз­личных способов представления чисел в ЦСФ, шумы последние рассмотрим только для случая представления чисел с фиксированной запятой и выравниванием слева в дополнительном коде.

Анализ прохождения шумов амплитудного квантования входных сигналов y(t) на выход ЦСФ может быть произведен путем их представления в виде суммы неквантованного дискретного сигнала и шума квантования . Так как ЦСФ является линейным уст­ройством, то сигнал на его выходе будет суперпозицией выходного дискретного сигнала Z_K и выходных шумов . Справедливость такой аддитивной модели обусловлена независимостью шума  с последовательностью точных выборок у_к. Кроме того, в отношении шумов квантования  в соответствии с подразделом 2.6 могут быть   сделаны   следующие   предположения:

шумы  являются стационарным    случайным процессом типа квазибелый шум с некоррелированными выборочными значениями;

плотность вероятности распределения значений  является рав­номерной во всем диапазоне  их возможных значений.

При данных предположениях анализ существенно упрощается.

Так   как

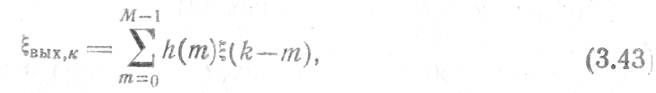
где h(m) —действительная импульсная характеристика ЦСФ;

М — число временных выборок входного сигнала, то ввиду -коррелированности выборочных значений шума квантования входных сигналов получаем среднее значение и дисперсию первой составляющей   выходного   шума   ЦСФ

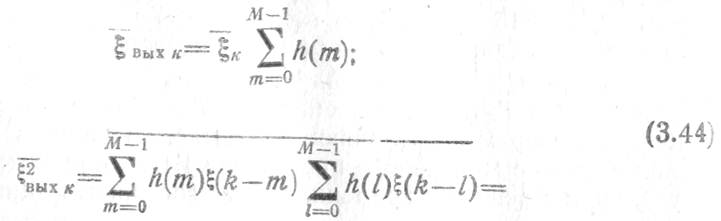
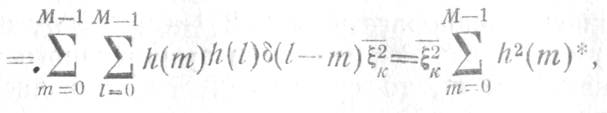
где —дисперсия шумов амплитудного квантования входно­го сигнала на единичном сопротивлении   (2.11).

Используя равенство Парсеваля, эти результаты можно пред­ставить   в   виде

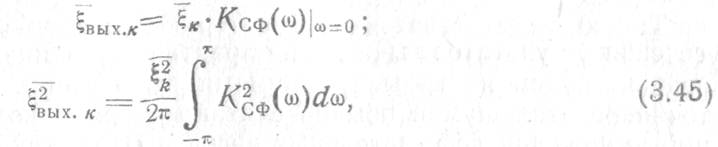
где  — амплитудно-частотная  характеристика  ЦСФ.

Так как обычно , а значения h²(m) только положитель­ные, то из данных выражений следует, что среднее значение шу­мов амплитудного квантования на выходе ЦСФ равно нулю, а их дисперсия растет с увеличением числа временных выборок вход­ного сигнала и шага амплитудного квантования . Напомним (подразд. 2.6), что последний определяется, с одной стороны, чувст­вительностью приемного устройства, а с другой — требуемым ди­намическим   диапазоном   по   входу   АЦП.

Рассмотрим следующий источник собственных шумов ЦСФ— шумы, вызванные округлением (усечением) результатов выпол­нения арифметических операций в выходных регистрах умножи­телей и сумматоров. Необходимость такого округления (усечения) обусловлена возрастанием числа разрядов представления этих результатов, особенно при выполнении операции умножения. Бу­дем считать, что числа до выполнения арифметической операции имели «L» разрядов, стоящих справа от двоичной запятой, а истин­ный результат R ее выполнения должен быть представлен «L₁» раз­рядами (L₁>L). Тогда под усечением понимают отбрасывание на­именьших значащих (L₁—L) разрядов, а при округлении такое отбрасывание сопровождается сравнением отбрасываемой вели­чины R— R₀ с половиной младшего разряда оставшегося L-раз­рядного числа (R—R₀—2^-L-1), которое при положительном ре­зультате сравнения увеличивается на 2^-L. Если обозначить число, получившееся после округления (усечения) через R₀(R_V), то ошибки усечения (l_y= R_y—R) и округления (l₀ = R₀—R) будут принимать   значения

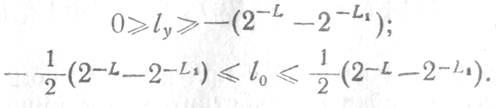
Так как можно предполагать, что , а статистика ошибок /о(/_у) такая же, как у шумов амплитудного квантования входных сигналов (2.7), то средние значения и дисперсии этих ошибок   будут   равны

Так как статистические характеристики ошибок округления и усечения результатов вычислений практически одинаковы, то в даль­нейшем будем их называть шумами вычислений. Количество ис­точников этих шумов обычно считают равным количеству опера­ций умножения действительных чисел в ЦСФ, так как шумы сум­мирования (вычитания) можно исключить сравнительно неболь­шим увеличением количества разрядов арифметических устройств по сравнению с разрядами чисел на выходе АЦП. Это также поз­воляет уменьшить дисперсии ошибок (3.46), вносимых при ап­проксимации произведений, по сравнению с дисперсиями ошибок амплитудного   квантования   входных   сигналов    .

Как правило, значения корреляционной суммы на выходе ЦСФ представлены в комплексной форме (3.27, 3.32). Определим ошиб­ку вычислений е при одном комплексном умножении. Для этого в качестве примера рассмотрим вычисление одного из слагаемых прямого   ДПФ    (3.32а)

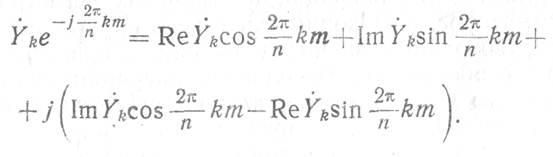
Результат округления этого комплексного произведения будет равен

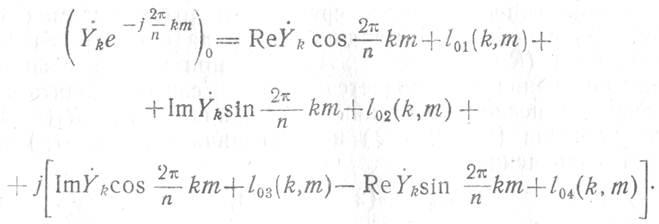
Определяя ошибку вычислений е при комплексном умножение, будем полагать, что ошибки   действительных умножений имеют одинаковые дисперсии и некоррелированы между собой, а так­же некоррелированы со входным, а, следовательно, и с выходным сигналами. Тогда среднее значение и дисперсия ошибок вычис­лений е при округлении одного комплексного произведения будут равны

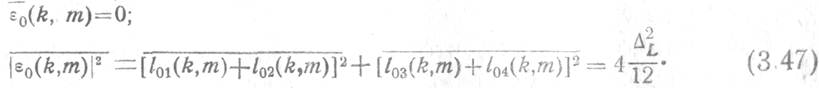
Очевидно, аналогичный результат будет иметь место и при определении ошибок вычисления корреляционной суммы в ЦСФ во   временной   области    (3.27).