Приемно-передающие устройства радио­технических систем: Учебное пособие, страница 7

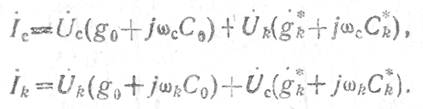
Сопоставив эти соотношения с уравнениями линейного четырехполюсника  , легко найти внутренние параметры  эквивалентного линейного четырехполюсника с переменными параметрами

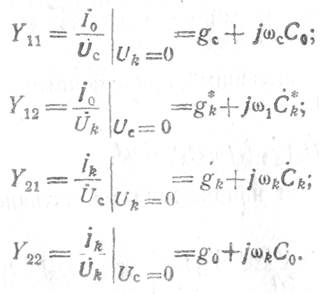
Рассмотрение коэффициентов, входящих в уравнениечетырех­полюсника с переменными параметрами, показывает, что в ряде случаев при отрицательных индексах k и ω_с <  |kω_r | комбинаци­онные частоты являются отрицательными. Физически это соответ­ствует обращенным спектрам на комбинационных частотах, ко­торые являются зеркальным отображением спектра сигнала от­носительно частоты 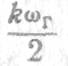 (рис. 1.15).

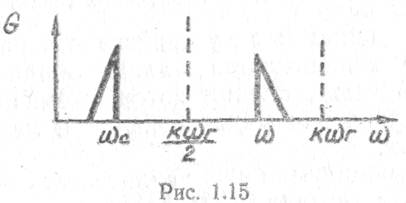
При этом каждая спектральная составляющая сигнала на комбинационной частоте имеет сдвиг по фазе на π. Если учесть знак частоты в соотношениях для i_c   и i_k, то они приобретают следующий вид:

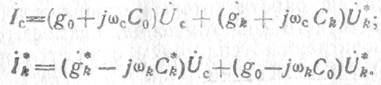
При этом учтено, что

Приведенный анализ можно обобщить на случай каскада с переменными параметрами, имеющего произвольное число конту­ров, настроенных на комбинационные частоты ω_c+kω_r. Произво­дя отбор коэффициентов, соответствующих этим частотам, можно получить систему N уравнений, связывающих комплексные ам­плитуды токов и напряжений на .выбранных комбинационных частотах. Коэффициенты при соответствующих напряжениях об­разуют матрицу проводимости многополюсника с переменными параметрами.

Зная эти коэффициенты, можно по известным формулам внеш­них параметров определить последние для каждого конкретного случая резистивной или емкостной связи настройки выходного контура и соотношения частот ω_с   и kω_г.

Такой важный внешний параметр, как коэффициент шума, может быть найден по известной формуле коэффициента шума линейного четырехполюсника

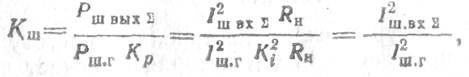
где I²_BX∑  - сумма средних квадратов шумовых таков всех ис­точников шума, пересчитанных к входу четырехполюсника;

I²_шг— средний квадрат шумового тока источника сигнала.

Изложенные .выше вопросы общей теории линейного шумяще­го каскада с переменными параметрами дают возможность ана­лизировать любые реальные линейные радиотехнические устрой­ства, содержащие элементы с переменными параметрами.

1.2.3. Анализ линейных регенеративных усилителей

В современных приемных устройствах радиотехнических средств вооружения используются малошумящие усилители вы­сокой частоты, механизм усиления которых значительно отлича­ется от механизма усиления радиосигналов в ламповых и тран­зисторных усилителях.

Большой класс малошумящих усилителей, обеспечивающих усиление на частоте сигнала, использует явление регенера­ции (частичной компенсации потерь) в цепи сигнала, возникаю­щее за счет внесения отрицательного сопротивления. Внесение в колебательный контур отрицательного сопротивления эквива­лентно повышению его добротности. Такое явление называется регенерацией. Усилители, работа которых основана на внесении в их контур отрицательного сопротивления, называются регене­ративными. К регенеративным усилителям относятся параметрические, туннельные и квантовые усилители.

Особенность регенеративных усилителей состоит в том, что источник сигнала и нагрузка включены в общую цепь и по отно­шению к ним усилительный элемент является двухполюсником. Все регенеративные усилители, независимо от принципа получе­ния регенерации, обладают рядом общих свойств. Анализ харак­теристик усилителей возможен при использовании соотношений, полученных при анализе линейных каскадов с постоянными параметрами. Для этого в эквивалентной схеме (рис. 1.9) необхо­димо учесть влияние положительной обратной связи.

Эквивалентная схема усилителя при этом приобретает вид (рис.   1.16).

Колебательный контур в схеме настроен на частоту   сигнала и имеет активную проводимость g₀₁, которая включает в себя потери в контуре и активную составляющую входной   статической проводимости каскада.

Величина   отрицательной   входной    проводимости     четырехпо­люсника определяется выражением

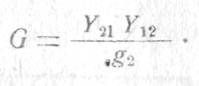
Как видно из рисунка 1.16, коэффициент передачи мощности пропорционален коэффициенту отражения на входе Г²_ВХ

Учитывая, что мощность сигнала и отраженной волны рассеи­вается на проводимостях источника сигнала и нагрузки пропор­ционально отношению проводимостей 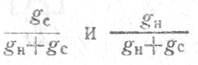 в терминах Y-параметров, можно записать

,

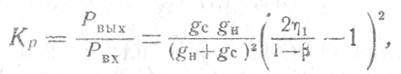где

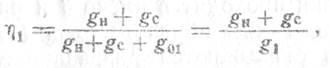
g₁=g_и+g_с+g₀₁ - полная проводимость потерь.

Проводя преобразования, с учетом того, что g₁≈g_с+g_н , полу­чим:

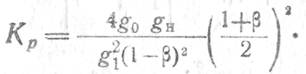
При β, близком к единице,

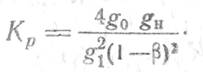
Рассмотренный режим работы регенеративного усилителя на­зывается режимом «на проход». В этом режиме при равенстве проводимостей источника сигнала и нагрузки

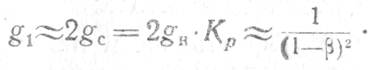
Для повышения коэффициента усиления регенеративного уси­лителя при неизменном коэффициенте β необходимо найти спо­соб разделения падающих и отраженных волн, исключив потери рассеяния их мощности на проводимостях g_c и g_н. Для этой цели используются ферритовые вентили и циркуляторы.

Эквивалентная схема регенеративного усилителя с циркулятором показана   на   рис. 1.17.

Сигнал через плечи I—2 циркулятора поступает в линию, на­груженную на колебательный контур L_э С_Э шунтированный про­водимостью потерь g₀₁  и отрицательной проводимостью G

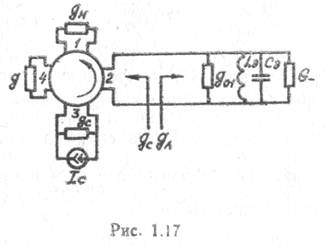
Отраженная волна сигнала через плечи 2—3 циркулятора полностью поступает на нагрузку g_н. Отраженные волны в этом плече и шумы нагрузки проходят в плечо 3 и рассеиваются на со­гласованной нагрузке. Таким образом, вход 1 и выход 3 регене­ративного усилителя оказываются развязанными между собой, а его коэффициент передачи при идеальном циркуляторе в точ­ности равен квадрату коэффициента  матрицы рассеяния S₁₁:

,

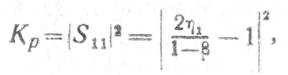где

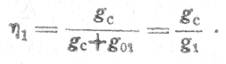
При большой регенерации β→1 и g_c≈g₁

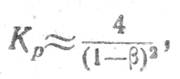
что в четыре раза больше, чем К_р, в режиме «на проход».

Рассмотренныйрежим работы регенеративного усилителя на­зывается режимом «на отражение», а усилители — отражатель­ными.

Полоса пропускания и эффективность регенеративного усили­теля полностью определяются резонансными свойствами фи­льтра на частоте сигнала и частотной зависимостью отрицатель­ной проводимости. Если отрицательная проводимость G в поло­се сигнального фильтра не зависит от частоты, то полоса пропус­кания РУ определяется выражением

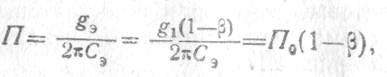
что  справедливо  для  усилителей    проходного  и  отражательного типа. При этом