Ответы на экзаменационные вопросы № 1-75 дисциплины "Экономика" (Функции экономической теории. Налоговая политика: кривая Лаффера), страница 98

Существуют два типа экономического роста:

- интенсивный;

- экстенсивный.

Интенсивный тип экономического роста осуществляется за счет совершенствования техники и технологии, за счет увеличения производительности труда, представляющей собой выработку одного работника в единицу времени. При интенсивном типе:

Y_t – объем производства за период времени t;

Y_t-1 – объем производства за период времени t-1;

N_t – объем занятости за период времени t;

N_t-1 – объем занятости за период времени t-1.

Экстенсивный тип экономического роста достигается путем привлечения дополнительных факторов производства, в частности, увеличения трудозатрат, измеряемых в человеко-часах.

В реальной действительности экономический рост осуществляется одновременно как за счет совершенствования техники и технологии, так и за счет вовлечения дополнительных факторов производства. В связи с этим следует говорить или о преимущественно интенсивном, или о преимущественно экстенсивном типе экономического роста. Если экономический рост происходит в большей степени за счет увеличения производительности труда, например на 70%, то это преимущественно интенсивный тип, если за счет увеличения трудозатрат (на 70%), то это преимущественно экстенсивный тип экономического роста.

Модель Солоу

Модель, разработанная в 1956 г., является простой моделью, в которой представлены только домохозяйства и фирмы.

Модель основана на принципе совершенной конкуренции, полной занятости и  взаимозаменяемости факторов производства. Уровень цен в модели является гибким.

В основе модель лежит производственная функция:

                                 , где                           (123)

Т – это параметр, отражающий уровень технологии.

Без учета технического прогресса, то есть при постоянной технологии, данная производственная функция в расчете на душу населения может быть представить как:

                                    ,где                                    (124)

у – показатель, отражающий производительности труда (Y/N);

k – показатель, отражающий капиталовооруженность труда (K/N).

График производственной функции в расчете на душу населения представлен на рис. 59.

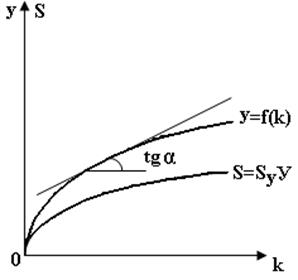
Рис. 59. Производственная функция Солоу и функция сбережений.

Прирост капитал находится по формуле:

                                    ,где                                    (125)

d – норма амортизации.

В условиях статического равновесия инвестиции равны сбережениям (I = S), то есть можно записать:

                                                                                   (126)

Формулу (125) может быть представлена:

                                                                       (127)

В расчете на душу населения эта формула примет вид:

                                                                         (128)

Равновесие в модели Солоу будет достигаться в том случае, когда уровень капиталоемкости будет оптимальным, при котором будет достигнута максимальная производительность капитала. Для обеспечения динамического равновесия оптимальный уровень капиталоемкости на душу населения не должен меняться, то есть должно выполниться условие:

                                                                                        (129)

Условие (129) будет достигнуто при выполнении равенства:

                                                                                  (130)

Используя формулу (124) уравнение (130) может быть записано следующим образом:

                                                                            (131)

Динамическое равновесие представлено на рис. 60.