Экономика и менеджмент \ Экономика

Ответы на экзаменационные вопросы № 1-75 дисциплины "Экономика" (Функции экономической теории. Налоговая политика: кривая Лаффера), страница 73

, где

(31)

X – объем производства какой-либо отрасли;

У – конечный продукт данной отрасли:

А – матрица технологических коэффициентов аiк.

Когда эти коэффициенты расставляются в системе уравнений, которые решаются одновременно, составляется третий квадрант (таблица), называемая «инверсией Леонтьева», которая показывает, что требуется от каждого сектора для приращения общего выпуска на один доллар.

Применение инверсии, во-первых, приводит к улучшению положения при сборе международных экономических и статистических данных, во-вторых, раскрывает работу внутреннего механизма хозяйства, в-третьих, способствует проведению анализа экономической политики, поскольку она показывает, что требуется от каждого сектора в виде затрат для увеличения выпуска данных товаров.

В общих чертах модель «затраты-выпуск» представляет собой таблицу структуры валового национального продукта.

Затраты каждой отрасли отражены по вертикали, что характеризует потребление (формирование затрат) промежуточной продукции каждой отраслью и ее вклад в создание конечного продукта.

По горизонтали в таблице отражен выпуск продукции по отраслям, что отражает отраслевую структуру потребления (распределения) промежуточного продукта и конечного продукта отрасли. В строках и столбцах в одинаковом порядке перечислены одни и те же отрасли материального производства от 1 до n.     

В таблице 1 представлена модель «затраты-выпуск» по методу В. Леонтьева.                      

   Таблица 1

Модель «затраты-выпуск»                              

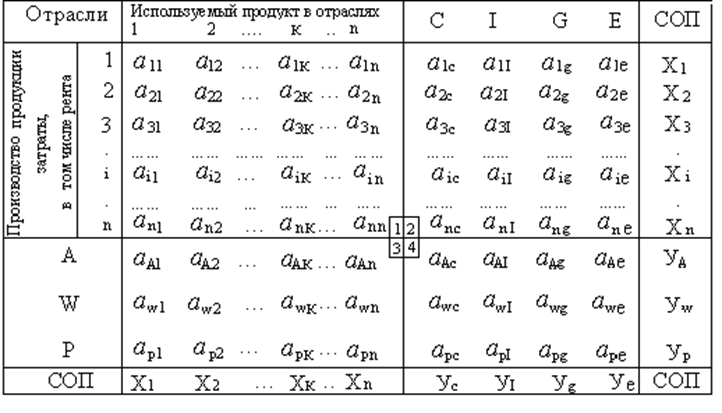
где:

n – количество отраслей,

i – i –ая отрасль, поставляющая промежуточный продукт;

к – к-ая отрасль, потребляющая промежуточный продукт;

СОП – совокупный общественный продукт;

А – амортизация;

W – заработная плата;

P – прибыль;

C – потребительские расходы;

I – инвестиционные расходы;

G – государственные расходы;

E – чистый экспорт.

1-ый квадрант

а11 – продукция, произведенная в первой отрасли и потребляемая в первой отрасли;

а21 – продукция, произведенная во второй отрасли и потребляемая в первой.

2-ой квадрант

а1с – продукция первой отрасли, которая идет на потребление;

а1I – продукция первой отрасли, которая идет на инвестиции;

а1g – продукция первой отрасли, которая идет на государственные расходы;

а1Xn – продукция первой отрасли, которая идет на экспорт.

3-ий квадрант

аa1 – амортизационные отчисления в 1-ой отрасли;

аw1 – заработная плата, выплачиваемая в 1-ой отрасли;

ap1 – прибыль, получаемая 1-ой отраслью.

4-ый квадрант

аac – амортизационные отчисления, идущие на личное потребление (обычно равны 0);

аaI – амортизационные отчисления, идущие на инвестиционные расходы;

аag – амортизационные отчисления, идущие на государственные расходы (обычно равны 0);

аwc – заработная плата, которая идет на личное потребление;

a wI – заработная плата, идущая на сбережения;

awg – заработная плата в государственном секторе;

apc – прибыль, идущая на потребительские расходы (премии);

apI – прибыль, идущая на инвестиционные расходы;

Исходя из таблицы 1, условие равновесия в экономике можно записать в следующем виде (32): 

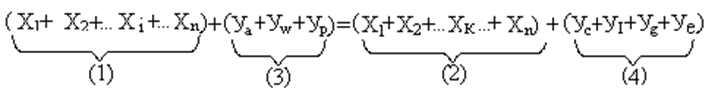
Скобка (1) отражает затраты на производство промежуточного продукта.

Скобка (2) показывает промежуточный продукт, который используется всеми отраслями.

Скобка (3) отражает добавленную стоимость всех отраслей.

Скобка (4) показывает конечный продукт всех отраслей.

Скобка (1) и скобка (2) равны друг другу, тогда условием равновесия будет:

(32)

При разработке метода «затраты-выпуск» В. Леонтьев использовал опыт первого русского баланса народного хозяйства ЦСУ СССР («Баланс народного хозяйства СССР в 1923/24 гг.», опубликованный в 1926 г.), который оказал на него значительное влияние. Создатели баланса народного хозяйства, в свою очередь, исходили из схем воспроизводства К. Маркса, так как именно он был автором первого шахматного баланса, разработанного им в экономических рукописях 1857-59 гг.

3. Неоклассическая модель общего экономического равновесия. Недостатки модели.

Скачать файл