Ответы на экзаменационные вопросы № 1-75 дисциплины "Экономика" (Функции экономической теории. Налоговая политика: кривая Лаффера), страница 92

d – норма амортизации;

i – ставка процента;

(d+i) – представляет собой альтернативные затраты средств в качестве капитала MOC (marginal opportunity cost).

Таким образом, предприниматель будет осуществлять инвестиции в таком объеме, чтобы величина имеющегося у него капитала уравнялась с оптимальной (К*), при которой предельная производительность капитала равна альтернативным затратам средств в качестве капитала, а прибыль – максимальна.

С учетом износа основного капитала формула (95) примет вид:

dK – амортизация капитала.

1. Базовая теория инвестиций с учетом налогов и субсидий

(Дейл Йоргенсон и Роберт Холл (США)1967 г.

и Лоренс Саммерс (США) 1981 г.)

Выплата налогов и субсидий влияет на принятие оптимальных инвестиционных решений. При введении налоговой ставки на прибыль в размере t предельная производительность капитала будет равна r* (1-t). Если при этом имеются какие-либо налоговые льготы, субсидии или ускоренная амортизация, то формула (96) примет вид:

t – налоговая ставка на прибыль;

s – доля цены инвестиционных товаров, отражающая льготное налогообложение, то есть экономию от инвестиционных налоговых льгот, а также от снижения налогов за счет ускоренной амортизации и вычета процента из налогооблагаемой суммы.

Если (s > t), то произойдет поощрительное стимулирование инвестиций. Это следует осуществлять в условиях низкой инвестиционной активности.

Если (s < t), то произойдет ограничение прироста инвестиций, что следует делать в условиях «перегрева» в экономике.

2. Модель акселератора инвестиционного процесса

(Дж.М. Кларк (США)1917г., П. Кларк (США) 1979 г.

и О.Дж. Бланшард (США) 1981 г.)

В основе модели лежит предположение, согласно которому существует устойчивая зависимость между необходимой величиной капитала и объемом выпуска, то есть что оптимальный размер капитала представляет собой постоянную долю (α) объема производства:

Данное равенство верно лишь при незначительном изменении стоимости капитала, то есть когда величина (d+i) меняется незначительно. Отсюда формула (95) примет вид:

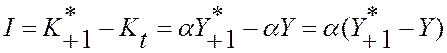, где             (100)

Данная формула показывает, что инвестиции растут в том случае, если ускоряются темпы роста производства.

С учетом амортизации формула (100) будет записываться следующим образом:

                                                           (101)

Теория имеет ряд недостатков. Во-первых, величина (α) рассматривается как постоянная величина. Однако при значительном изменении стоимости капитала (d+i) показатель (α) тоже изменится. Во-вторых, величина капитала достигает оптимального уровня не сразу, а постепенно из-за того, что не всегда имеются для этого достаточные инвестиции. В-третьих, величина инвестиций определяется исходя из ожиданий, поскольку будущий объем выпуска продукции неизвестен, а ожидания могут быть неверными и изменчивыми. Тем не менее, данная теория достаточно точно объясняет структуру и динамику инвестиций.

3. Теория инвестиций на основе издержек регулирования

 (Р. Эйснер и Р. Стротц (США) 1963 г., Р. Лукас (США) 1967 г.)

В реальной действительности требуется время для того, чтобы достичь оптимального размера капитала, при котором прибыль будет максимальной. Стремление к максимизации прибыли изменяет величину основного капитала постепенно из-за технических ограничений возникающих при реализации инвестиционного проекта. По расчетам экономистов (П. Кларк) инвестициями в течение года предприниматели могут обеспечить преодоление только трети разницы между фактическим и желаемым объемами капитала.

Согласно  теории инвестиций, основанной на издержках регулирования, существует механизм частичного регулирования, описывающий постепенное приближение капитала К и оптимальному уровню К*: