Обсуждение конкретных задач (например, разработка корректной инженерной методики расчета эжекторов "газ-газ") будет дано в последующих публикациях автора.
Обсудим другие возможные варианты выбора обобщенных переменных P,T9V и соответственно обобщенных показателей адиабаты .
187
Попытаемся, например, несколько "улучшить" канонический показатель S, введя обобщенный удельный объем (сохранив при этом температурную переменную Т): V - V + К„, где Vo - некоторый подго-ночный параметр, который может зависеть и от температуры Обобщенный показатель S определится следующим образом:
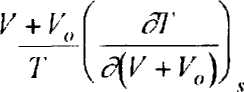
Рассмотрим частный случай, когда Vo не зависит от температуры. Тогда S выразится через Sw Vo очень просто:
8 -\ = {S-\{\+— \ = (S-\{\+-V°\ (20)
V Vo) у У zRTJ
Анализируя соотношение (20), нетрудно видеть, что в ограниченной области температур и давлений некоторое отрицательное значение параметра Vu позволяет обеспечить квазипостоянство д на изоэн-гропах. Однако с ростом температуры (и давления) на изоэнтропе происходит как бы "срыв" обобщенного показателя, и 5 начинает достаточно быстро уменьшаться.
Аналогично, введя в рассмотрение "обобщенное" давление
Р - Р + а/ (V + Ь),2 можно определить обобщенный показатель £ по формуле (5).
В технических приложениях получили широкое распространение кубические уравнения состояния ван-дер-ваальсового типа, например, уравнения состояния типа Редлиха-Квонга (особенно в модификациях Соаве и последующих авторов). Уравнение состояния типа Редлиха-Квонга в принятых выше обозначениях можно записать следующим образом:
PV = RT, Р = Р +---------- , V = V-b, 7 = T.----------------------------- (21)
V(V + b)
Такая форма записи обобщенных переменных I\T,V «индуцирует" обобщенный показатель адиабаты £ :
к =
v-ъ
![]() Р + а/ V(V + h)
Р + а/ V(V + h)
-In а
(22)
188
По аналогии с вышеизложенным можно сказать, что в записи (21) кубические уравнения состояния "индуцируют" обобщенный показатель адиабаты, промежуточный между каноническими показателями г, и 5, т.е. аналогичный введенному выше обобщенному показателю ц-типа, поскольку в (22) сохраняется температурная переменная (Т = Т). Отметим (но оставим в данной публикации без дополнительного анализа) определенную неоднозначность введения обобщенных переменных Р,7\Р, ассоциированных с каким-либо конкретным уравнением состояния. Например, то же уравнение состояния Редли-ха-Квонга (22) можно представить и в таком виде:
![]()
![]() v(v+by ' ~ \-biv'
v(v+by ' ~ \-biv'
По-видимому, целесообразно сформулировать задачу конструирования новых классов уравнений состояния (например, кубических или близких к ним по своей структуре), "обеспечивающих" квазипостоянство "индуцированного" ими обобщенного показателя адиабаты. Эти важные аспекты здесь далее не обсуждаем, отметив только, что в констексте нашего обсуждения общий подход к их рассмотрению представляется достаточно ясным.
Таким образом, в работе введен в рассмотрение и проанализирован класс обобщенных показателей изоэнтропы (адиабаты) реального газа. Найдены мало меняющиеся на изоэн-тропах показатели в широком диапазоне изменения переменных P,T,S. Практическое применение предложенной системы обобщенных показателей адиабаты состоит в возможности использования простых, но достаточно точных соотношений термогазодинамики реального газа и получении при этом инженерных методик расчета повышенного класса точности для газодинамических процессов, протекающих в компрессорах, эжекторах, турбодетандерах и др. устройствах. Погрешность подобных приближенных формул (при сравнении с формально "точным" расчетом в рамках одномерной термогазодинамической модели течения) в типичных случаях, по нашим оценкам, составляет -0,1-0,3 %. Кроме того, вышеизложенный подход к построению термогазодинамики реального газа имеет, на наш взгляд, определенный методический интерес и вполне может использоваться в учебном процессе в соответсвующих разделах курсов технической термодинамики и газодинамики.
189
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.