Дифференциальные уравнения движения флюида
Дифференциальную форму закона сохранения массы можно получить из интегральной (2), используя формулу Остроградского-Гаусса, согласно которой
J pvnds = J di vpVdV.
s i'
После подстановки этого равенства в уравнение (2) получаем интегральное уравнение
В силу производительности объема для выполнения равенства необходимо, чтобы
p 0. (24)
Уравнение (24) представляет собой дифференциальную форму уравнения, выражающего закон сохранения массы.
Это же уравнение легко получить, приняв в (Г) M-pdV.
Уравнение (24) может быть записано в координатной форме, например:
• в системе криволинейных триортогональных координат аД г'(рис.2).
ск
где На, Нр, Нт - коэффициенты Ламе в выражениях для элементов длины координатных линий
dla-Hada, dl^= H^dp, dly=Hydr, (26)
v«, v/u Vy - проекции скорости флюида на касательные к координатным линиям; £,, г[, <; - единичные векторы вдоль касательных к координатным линиям:
• в декартовой системе
координат
(а =у, р - х, г = z) На
= Н^ = Ну=1.
Следовательно,
ф | <%pvx) i ^РУу)|
d ск ду
• в цилиндрической системе координат (a=r, p=(p, y=z) H^=r,
97
|
|
|
п ^ |
|
бок |
98
Рис. 1. Схема элемента горизонтального ствола
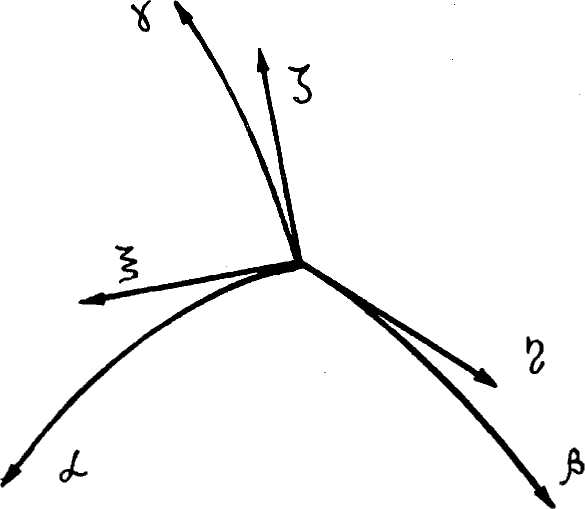
Рис. 2. Система криволинейных координат
1; отсюда
dt cfr ' r dcp az
Перейдем к выводу дифференциального уравнения сохранения количества движения. В соответствии с общей формулировкой закона сохранения количества движения запишем уравнение (3) в виде
p^ или ЛК = (>аР+/>)Л*. (29)
Dt
где Р - поверхностная сила, отнесенная к единице объема.
В соответствии с определением субстанциальной производной приращение количества движения складывается из локальной составляющей, учитывающей нестационарный характер течения, и конвективной составляющей, учитывающей перемещение частиц потока. Локальная составляющая изменения за промежуток времени количества движения массы, заключенной в криволинейном параллелепипеде (рис.3) равна
ДК = ^—t На НрН7 AaAflAyAi, (3 0)
Конвективная составляющая определяется как разность количества движения масс, входящих и покидающих криволинейный параллелепипед за промежуток времени At, в следующем виде:
ЛК = Аа[{руаМрНг )Д//ДГ]Д/ + А^(ру^НаН^АаАу]А( +
где А „, Ар, Ду разность значений выражения при a -0 и Да, р=0 и Ар, у = О И Лу.
Суммируя уравнения (30) и (31 ^получаем общее изменение ко личества движения массы за единицу времени:
да
(32)
AaAfiAy.
Уравнение (32) определяет члены, входящие в левую часть уравнения сохранения количества движения (29). Определим силы. входящие в правую часть этого уравнения. Значение объемной силы,
99
|
|
|
N. |
|
N |
|
dp, |
too
N
Рис. З. Криволинейный параллелепипед
действующей на элементарный криволинейный параллелепипед, равно
рРНаНрНуАаАрАу,(33)
где На Щ RyAaAflAy равно объему элементарного криволинейного параллелепипеда.
Результирующую поверхностных сил представим в виде
R = ZRa+tjRfi + &ri(34)
где Ra, Rp, R7 - проекции поверхностных сил на оси а, р, у соответственно. Как показано в работе В.З.Власова [12], эти проекции равны
ка
а да
,-Н.
да
да
д
[Р
а
ду
АаА/ЗАу\
(35)
д
(36)
Р
да
AaAfSAy,
д
д
![]()
![]() а
а
тау
c\\
АаАРАу
ду
(37)
После подстановки (32-37) в (29) получаем дифференциальное уравнение сохранения количества движения
|
д |
d(pv)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.