Вопросы методологии и новых технологий разработки месторождений природного газа. Часть III (Сборник научных трудов), страница 118

др₂/дх -

(4)  (5)

Из (2) на основании (3) имеем

т.е. суммарный дебит q = q?+q₂ - q(t) зависит только от времени:

я= я(0-                                   (6)

Подставляя (4) в (1), получаем

к₇у₂

(7)

 \ Зс

 дх.

так как

Складывая правые и левые части формул (7), учитывая (6) и подставляя в (1) и (2), получаем дифференциальное уравнение движе­ния границы раздела при вытеснении жидкостью 1 жидкости 2.

д

У-

-- + tga

= m((J_H-a_o)-j-, at

(8)

где

Если жидкость 2 вытесняет жидкость 1, то все основные соот­ношения, используемые при выводе дифференциального уравнения движения границы раздела при вытеснении жидкости 2 жидкостью 1, остаются без изменения, за исключением уравнений неразрывности, которые в этом случае имеют вид

dq,/dx = т • (ст_н - а_о) • dy_}/dt;   dq₂/dx = m ■ (а„- а_о) • dyjdt,

и соответственно дифференциальное уравнение движения границы раздела при вытеснении жидкости 1 жидкостью 2 примет вид

277

д_

У

к_? .        ,,     J ду
q------- Aycosa{h - у)\ -— + tga

(9)

где а_о* - остаточная насыщенность жидкостью 1.

Дифференциальные уравнения (8) и (9) дополняются граничны­ми и начальными условиями, которые имеют вид:

• граничные условия - ду/дп=§ при х=х_в, ду/дп =0 при х=х_н; (10)

•          начальное условие - у = h • tga.           (11)
Т.е. мы предполагаем, что кровля и подошва пласта непроницае­
мы, а в начальный момент времени граница раздела представляет со­
бой горизонтальную плоскость.

Таким образом, задача о движении границы раздела двух жид­костей в вышеприведенной постановке сводится к решению нелиней­ных дифференциальных уравнений (8) и (9) с граничными (10) и на­чальным (11) условиями.

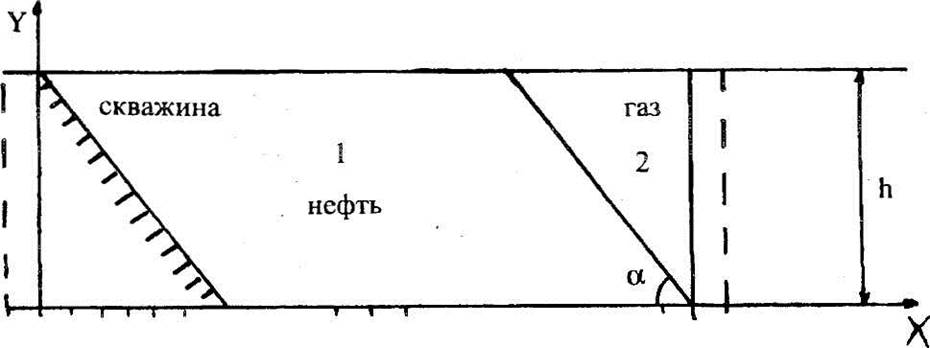
Задача решалась численно, с использованием метода конечных разностей по явной схеме. При этом получаются следующие соотно­шения (для случая вытеснения жидкостью 1 жидкости 2_} рис.2 ).

(12)

2 Ах                         '       А/

и случая вытеснения жидкостью 2 жидкости 1 (рис.2)

i

~   i

2Дх

^J- = m(<J_H - а_о

At

(13)

где

Ф■

 = У

--*- Aycosa(h - )_/+, !

tga

278

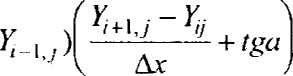
Граничные условия имеют вид:

• для случая вытеснения жидкостью 1 жидкости 2

У_Х=У_О   и  Y^=Y_H;

Рис.1. Расчетная схема к задаче о движении границы раздела в пологом пласте

о

5            -1          +1.           -1        +1

Рис.2. Схема дискретизации области фильтрации

279