Введем подвижную локальную систему координат (ЛСК) AXkYk, жестко связанную со звеном и движущуюся вместе с ним. Пусть координаты точки А(xA,yA) начала ЛСК в системе OXoYo известны, так же как и проекции скорости (VAxo, VAyo) и ускорения (aAxo, aAyo) этой точки. Кроме того, пусть известны: относительный угол jk, отсчитываемый от оси Xo до оси Xk против часовой стрелки, угловая скорость звена wk, и его угловое ускорение ek. Эти величины можно определить методом векторных контуров, как это описано выше.
Связь между координатами точки, измеренными в разных системах координат, в матричной форме записывается в виде:
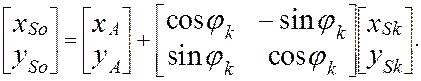
Последовательно дифференцируя выражение ( 2.36 ) по времени, получим зависимости для определения проекций скоростей и ускорений:
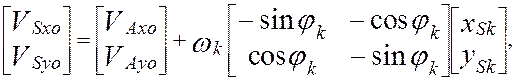
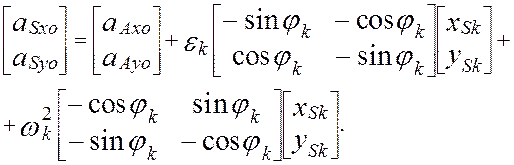
Координаты (xSk, ySk) являются конструктивными параметрами, величины (VAx, VAy), (aAxo, aAyo), jk, wk, ek , определяются методом векторных контуров, как это показано выше. Следовательно все элементы матриц в правых частях выражений ( 2.36 ), ( 2.37 ) определены.
Расстановка ЛСК на звеньях механизмов производится по следующим правилам.
1. Начало k-й системы помещается в ту точку k-го звена, кинематические параметры движения которой могут быть предварительно определены.
2. Ось Xk направляется вдоль соответствующего вектора lk (см. векторные контуры в п. 2.3) или параллельно ему, ось Yk - так, чтобы образовывалась правая система координат.
Вообще говоря, эти два правила определяют расстановку ЛСК неоднозначно. Конкретный вариант их расстановки зависит от того, кто реализует решение задачи. Применяемая в данном случае система расстановки показана на рис. 2.6, . . . 2.14. В пакетах ТММ_КР, GETMAN имеются разделы, где демонстрируется применяемые варианты расстановки ЛСК.
2.5. Общая последовательность кинематического анализа
Рассмотренные выше метод векторных контуров и метод преобразования координат позволяют произвести полный кинематический анализ механизма. Рассмотрим, как эти два метода взаимодействуют на примере 6-звенного механизма, представленного на рис. 2.16.
Общую последовательность кинематического расчета можно представить следующим образом. По исходно заданным кинематическим параметрам движения входного звена определяются параметры движения той его точки, в которой присоединяется 1-я структурная группа. Производятся расчеты для нее и вычисляются параметры движения той точки звена структурной группы, в которой присоединяется следующая. Эти значения преобразуются в систему координат следующей структурной группы, производится ее расчет и т.д.
Рассмотрим эту последовательность подробно. Пусть изначально задан угол поворота кривошипа ОА j01 от оси Xo, значение его угловой скорости w1, и ускорения e1 в данном положении.
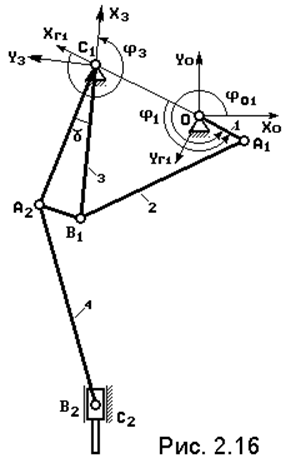Сначала решаем задачу для контура OA1B1C1,
состоящего из входного кривошипа и 3-х шарнирной структурной группы. Решение
производим в НСК OXГ1YГ1, естественной для данной группы
(см. рис. 2.16). Угол поворота кривошипа в этой системе:
j1 = j01 – y01, где: y01 – угол поворота системы OXГ1YГ1 от OX0Y0 :
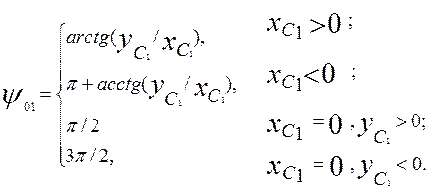
Координаты опоры С1(xC1, yC1) должны быть заданы как конструктивные параметры.
Параметры движения шарнира А1 определяем так, как это
описано в подразделе 2.2. Далее, производим анализ методом векторных контуров,
как это описано в п. 2.3.1. В результате находим j2, w2, e2, j3, w3, e3 – параметры движения шатуна А1В1
и коромысла В1С1. Методом преобразования координат (см.
подраздел 2.4) находим параметры движения центров масс этих звеньев и точки А2,
в которой присоединяется следующая структурная группа.
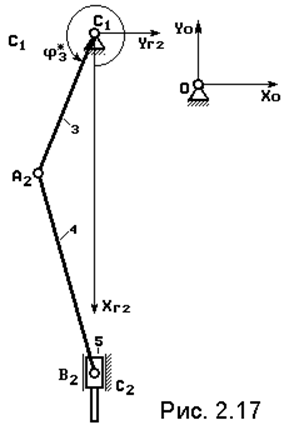
Переходим к следующему контуру C1A2B2, рассмотрим его отдельно (рис. 2.17). Он представляет собой 4-х звенный механизм со структурной группой типа “шатун-ползун”. Как показано в п. 2.3.2 решение удобно искать в НСК OXГ2YГ2, поэтому координаты шарнира А2, проекции его скорости и ускорения, найденные ранее в НСК OXГ1YГ1 следует преобразовать в НСК OXГ2YГ2, тогда контур C1A2B2 решается так, как это описано в п. 2.3.2. В результате находим j4, w4, e4 – параметры движения шатуна, C1C2, VC, aC – положение, скорость и ускорение ползуна. Методом преобразования координат находим параметры движения центров масс шатуна и при необходимости преобразовываем их в НСК XoYo.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.