Структурный анализ и синтез рычажных механизмов. Кинематический анализ рычажных механизмов. Динамика машин с упругими звеньями, страница 44

В рамках данных лекций мы рассмотрим только дискретные динамические модели механических колебательных систем. Введем некоторые основные понятия.

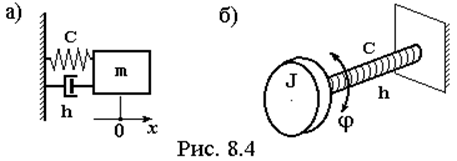
Жесткость – это свойство материалов противостоять деформациям. Коэффициент жесткости – количественная характеристика этого свойства. На рис. 8.4а показана одномассовая колебательная система и коэффициент жесткости упругого элемента обозначен буквой C. Если упругий элемент испытывает линейную деформацию, то по определению коэффициент жесткости – это сила, которую надо приложить к упругому элементу, чтобы деформировать его на единицу длины. В этом случае его размерность: [С] = [H/м].

Величина обратная коэффициенту жесткости называется податливостью:

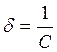Если упругий элемент испытывает деформацию кручения, как это показано на рис. 8.4,б, то коэффициент жесткости – это момент, который надо приложить к упругому элементу, чтобы деформировать его на единицу угла. В этом случае его размерность: [С] = [H м / рад] = [H м][4].

Демпфирование – это свойство материалов рассеивать энергию колебаний. Коэффициент демпфирования – количественная характеристика этого свойства. На рис. 8.4 он обозначен буквой h.

8.2. Собственные  колебания  одномассовой

линейной  консервативной  системы

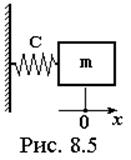
Консервативными называются динамические модели, которые не учитывают рассеяние энергии при колебаниях. Собственными называются колебания, которые совершает система, будучи однократно выведенной из состояния равновесия и предоставленная самой себе. На рис. 8.5 показана такая система.

Уравнение ее движения запишем на основании Принципа д’Аламбера. При одномерных собственных колебаниях на массу m действует только две силы: одна – это сила со стороны упругого элемента F_C, а вторая – это сила инерции F_И, то есть в данном случае д’Аламберово квазиравновесие имеет вид

F_C = F_И

Раскрывая выражения для сил, получаем:Cx = – ma

или                                                m + Cx = 0                                              (  8.1 )

Деля на массу, получаем

 + w₀²x = 0                                              (  8.2 )

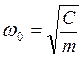где

– частота собственных колебаний.

Решение уравнения ( 8.2 ) имеет вид [ 12 ]:

x(t) = B₁cosw₀t + B₂sinw₀t                                (  8.3 )

Константы B₁ и B₂ найдем из начальных условий. Пусть x(0)= x₀, (0)= V₀ . Тогда из выражения ( 8.3 ) при t = 0 имеем

B₁ = x₀

Дифференцируем выражение ( 8.3 ) по времени

(t) = –B₁ w₀ sin w₀ t + B₂ w₀ cos w₀ t

и при t = 0 получаем  B₂ = V₀ /w₀

Существует и другая более наглядная форма записи решения ( 8.3 ):

x(t) = Asin(w₀t + a)                                     (  8.4 )

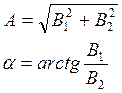где

– амплитуда колебаний,

– фаза колебаний.

Необходимо отметить, что консервативная система как модель для расчета колебательных процессов во времени не применяется, т.к. решение ( 8.3 ) или ( 8.4 ) это незатухающая синусоида, а любые свободные колебания обязательно затухают, т.к. в любой системе есть рассеяние энергии. Но с помощью этой модели мы получили фундаментальное понятие частоты собственных колебаний.

8.3. Приведение  коэффициентов  жесткости

при параллельном и последовательном соединении упругих элементов

При представлении реального объекта в виде дискретной модели деформируемые элементы конструкции представляют в виде упругих связей. При этом одна упругая связь конструктивно может состоять из различных элементов. Возникает задача вычисления единого коэффициента жесткости связи при известных коэффициентах жесткости элементов ее составляющих.

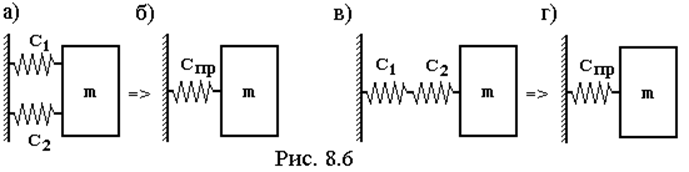
На рис. 8.6,а изображена ситуация, когда два упругих элемента стоят параллельно. В этом случае общий коэффициент жесткости (рис. 8.6б) равен сумме

C_ПР = C₁ + C₂                                        (  8.5 )

Необходимо отметить, что подобная операция корректна только в том случае, когда мы пренебрегаем поворотом массы m, и считаем, что ее движение приближенно можно считать поступательным.

На рис. 8.6в изображена ситуация, когда два упругих элемента стоят последовательно. В этом случае суммируются податливости: