Структурный анализ и синтез рычажных механизмов. Кинематический анализ рычажных механизмов. Динамика машин с упругими звеньями, страница 22

y = l_к (K_C+y’_i)( tg b_i cos y_i – sin y_i) – x tg b_i ,

y = x tg b_j – l_к (1/ K_C +y’_j)( tg b_j cos y_j + sin y_j),                              ( 4.26 )

x_O = l_к [(K_C + y’_i)(tg b_i cos y_i – sin y_i) +

+ (1/ K_C + y’_j)(tg b_j cos y_j + sin y_j)] / (tg b_i + tg b_j),

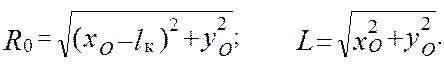
Таким образом, общая последовательность определения основных, габаритных параметров механизмов с коромыслом и роликом следующая. С достаточно мелким шагом строится диаграмма y’l_к (j) как это показано на рис. 4.13. Определяется количество точек этой функции, находящихся на фазе удаления – n₁, и на фазе возврата – n₂. Для каждого сочетания i = 1,2, ... n₁, j = 1,2, ... n₂, производятся вычисления по формулам ( 4.19 ) … ( 4.22 ) и запоминается вариант с наибольшим значением R_Omin. Если межцентровое расстояние L задано конструктивно то  R_O  определяют по формулам ( 4.23 ) … ( 4.25 ). В противном случае R_O  и L  находят по зависимостям ( 4.26 ).

Если значение R_Omin, полученное из условия ограничения угла давления, столь мало, что конструктивно не может быть реализовано, то в качестве R_Omin принимают конструктивно допустимую величину, а L определяют так, чтобы центр вращения кулачка располагался в допустимой зоне.

4.7.4. Механизмы  с  плоским  коромыслом

Схема такого механизма представлена на рис. 4.1,г. Для этих механизмов основными  геометрическими  параметрами являются пара (Ro, L), где Ro – радиус базовой окружности кулачка, L – межцентровое расстояние (между центром вращения кулачка и центром качания коромысла). Часто величина L для этих механизмов задается конструктивно, и в этом случае определению фактически  подлежит  только  Ro.

Также, как для механизмов с плоским толкателем здесь основные геометрические параметры определяют из условия выпуклости кулачка. Однако в данном случае нет возможности определить их так, как мы это делали выше. Объясняется это двумя причинами. В отличие от механизмов с плоским толкателем точка касания кулачка и коромысла имеет составляющую кориолисова ускорения и здесь не удается получить столь удобную зависимость для R_{o min} как формула ( 4.14 ). Но даже если бы и удалось ее получить, то такой диаграммы, какая представлена на рис. 4.11в для определения R_{o min} для механизма с плоским коромыслом построить невозможно, т.к. точка контакта коромысла с кулачком имеет сложную траекторию, которая может быть рассчитана только при известном  Ro .

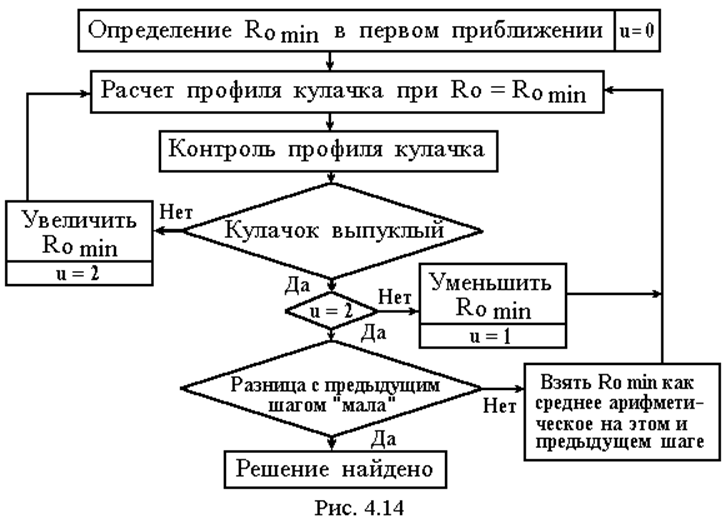
Преодолеть этот “заколдованный круг” можно с помощью итеративного алгоритма, представленного на рис. 4.14. Сначала по упрощенной методике, рассмотренной ниже, определяется может быть даже довольно грубое значение R_omin в первом приближении. Для этого значения R_o рассчитывается профиль кулачка, как это описано в п. 4.8.5. Производится контроль его выпуклости, по результатам которого организуется  следующая  итерация.

Рассмотрим определение R_{o min} в первом приближении. Методика строится по аналогии с определением R_{o min} для механизма с плоским толкателем, рассмотренным в п. 4.7.2. Расчетная схема представлена на рис. 4.15а. Пренебрегая кориолисовым ускорением и изменением рабочей длины коромысла l_к, строим график повернутого на –90^о аналога ускорения конца коромысла l_к^.y’’(y). Проводя через максимальное по величине значение на отрицательной ветви этой функции линию t-t под углом 45^о к оси  коромысла, на  линии ОА  находим  искомое  приближение

R^~_{o min} = l_к y’’_max – l_к y_i ,                                            ( 4.27 )

где y_i – угол поворота коромысла, при котором достигается y’’_max .

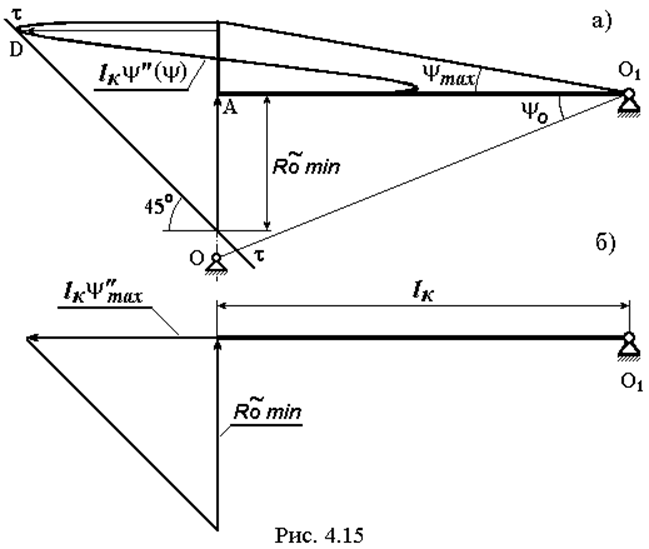Но поскольку мы ищем всего лишь начальное значение для запуска алгоритма на рис. 4.14, то можно поступить и еще проще, как это показано на рис. 4.15б и за начальное приближение принять максимальное по величине значение  аналога ускорения конца коромысла на отрицательной ветви функции l_к^. y’’(y):

R^~_{o min} = l_к y’’_max .                                            ( 4.28 )

Алгоритм поиска R_{o min} устойчивый и сходится даже при большой разнице  между  R^~_{o min}  и  фактическим  R_{o min}.

4.8. Расчет  профиля  кулачка