Структурный анализ и синтез рычажных механизмов. Кинематический анализ рычажных механизмов. Динамика машин с упругими звеньями, страница 35

гдеm_i – масса i-го звена, a_Si – ускорение его центра масс.

Например, для механизма на рис. 6.1 центры масс 2-го и 3-го звеньев имеют ускорения и возникают соответствующие силы инерции.

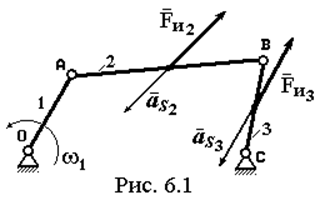Эти силы вызывают дополнительные реакции в кинематических парах, что увеличивает их износ. Кроме того, эти силы, переменные по величине и направлению, являются причиной вибраций, следовательно, появляется опасность резонансных явлений, которые могут привести к авариям. И, наконец, эти силы воспринимаются опорами механизма, через которые передаются на стойку. Последнее явление получило название внешней виброактивности механизма. Для таких устройств, как электро- и бензопилы, дрели, отбойные молотки и т.п. стойкой являются руки оператора, и такие воздействия могут привести к развитию так называемой вибрационной болезни. Из всего сказанного следует, что с этими воздействиями надо бороться.

Мероприятия, направленные на уменьшение описанных сил или компенсацию их воздействия на кинематические пары называется уравновешиванием.

Различают два типа уравновешивания:

1.  Статическое – компенсация воздействия сил инерции.

2.  Моментное – компенсация воздействия моментов сил инерции.

Совокупность статического и моментного будем называть полным уравновешиванием.

Как статическое, так и моментное уравновешивание в свою очередь подразделяют еще на:

1. Уравновешивание при известном расположении неуравновешенных масс.

2. Уравновешивание при неизвестном расположении неуравновешенных масс.

6.2. Уравновешивание  роторов

Ротор – это вращающееся звено, установленное в неподвижных опорах. Примерами роторов являются коленчатые валы двигателей внутреннего сгорания и дизелей, распределительные валы, роторы электродвигателей, турбин, колеса транспортных средств и т.п.

6.2.1. Уравновешивание роторов при известном расположении

неуравновешенных масс

Данная задача решается на этапе проектирования ротора. На рис. 6.2,а изображен некоторый вал, на котором расположены две неуравновешенные массы. На данном примере легко пояснить физический смысл статической неуравновешенности, который состоит в том, что центры масс деталей, установленных на роторе смещены относительно оси вращения и, как следствие, центр масс всего ротора тоже может быть смещен относительно этой оси. Таким образом, задачей статического уравновешивания в данном случае будет расчет и установка противовеса, так, чтобы центр масс всего ротора оказался на оси его вращения.

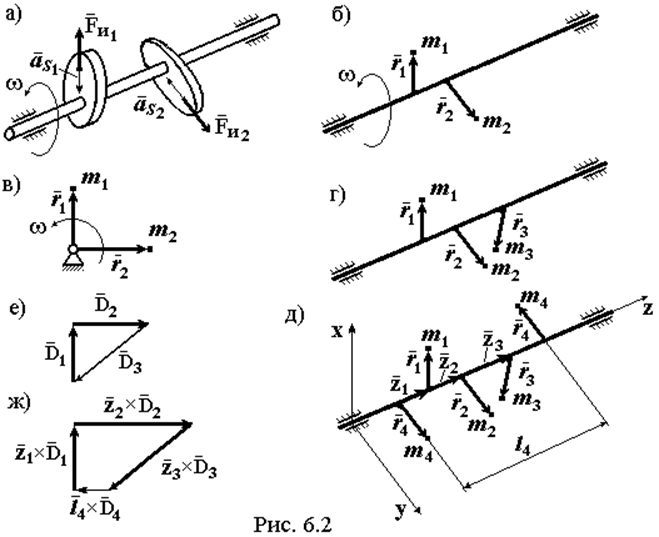На рис. 6.2б представлена расчетная схема, где m₁, m₂ – величины неуравновешенных масс, r₁, r₂ – радиусы расположения центров масс деталей, установленных на роторе. Вид с торца вала на систему показан на рис. 6.2в. Поскольку конструкция ротора известна, то значения m₁, m₂, r₁, r₂ могут быть рассчитаны, и мы их полагаем известными.

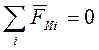Статическое уравновешивание. Условием статической уравновешенности является равенство нулю суммы всех сил инерции:

( 6.2 )

Из этого условия, полагая, что ротор вращается равномерно, получаем:

Произведение m_iмассы на радиус-вектор в теоретической механике называют статическим моментом массы, отсюда и название статическое уравновешивание. В инженерной практике для этого произведения укоренился другой термин: дисбаланс. Таким образом, окончательно условие статической уравновешенности получаем в виде равенства нулю суммы дисбалансов масс:

( 6.3 )

Собственно, статическое уравновешивание производится установкой противовеса. Для расчета его параметров построим план дисбалансов (см. рис. 6.2е ). Замыкая контур, получаем вектор характеризующий параметры противовеса. Конкретное сочетание значений m₃, r₃, обеспечивающее нужный дисбаланс подбирается конструктивно. На рис. 6.2г изображен ротор с установленным противовесом, статически уравновешивающим ротор.

Моментное уравновешивание. Условием моментной уравновешенности является равенство нулю суммы моментов всех сил инерции.

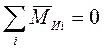
( 6.4 )

Введем систему координат XYZ (см. рис. 6.2д). Моменты сил инерции будем брать относительно начала координат этой системы: