Если не учитывать силу трения, то можно считать, что реакция R направлена по нормали к поверхности, в данном случае – к поверхности кулачка. Обратите внимание, что нормаль берется к центровому профилю кулачка, а точка контакта к – это конец толкателя или коромысла и ролик, даже если имеется, то не учитывается. VКТ – это скорость точки к, если считать ее принадлежащей толкателю.
На рис. 4.7 показан также угол передачи m, который является дополнительным до 90О к углу давления.
Угол давления является весьма важным параметром, т.к. если его величина превысит допускаемое значение, то КПД кинематической пары резко падает практически до нуля и кинематическую пару, а, следовательно, и весь механизм заклинивает. Предельно допустимыми значениями угла давления являются:
для механизмов с толкателем: [g] = 30 … 32О, для механизмов с коромыслом: [g] = 45 … 50О.
Таким образом, условием незаклинивания является: g£[g]. Соблюдение этого условия должно быть обеспечено еще на этапе проектирования механизма, а для этого необходимо выяснить какие размеры кулачкового механизма влияют на величину угла давления.
4.6. Связь между углом давления и основными геометрическими
параметрами кулачкового механизма
4.6.1. Механизм с толкателем центрального типа
 Это самый простой вариант. Расчетная схема для
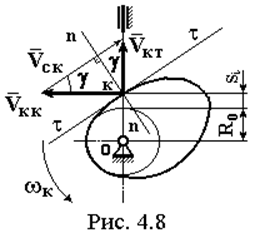
него представлена на рис. 4.8, где n-n
– нормаль к профилю кулачка в точке контакта кулачка и толкателя к, t-t –
касательная к профилю кулачка в этой же точке, g – угол давления. Механизм изображен в некотором
промежуточном положении на фазе удаления.
Это самый простой вариант. Расчетная схема для
него представлена на рис. 4.8, где n-n
– нормаль к профилю кулачка в точке контакта кулачка и толкателя к, t-t –
касательная к профилю кулачка в этой же точке, g – угол давления. Механизм изображен в некотором
промежуточном положении на фазе удаления.
На рис. 4.8 изображен план скоростей механизма, на котором приняты следующие обозначения:
VКТ – это скорость точки к, если считать ее принадлежащей толкателю,
VКК – это скорость точки к, если считать ее принадлежащей кулачку,
VСК – это скорость скольжения точки к толкателя по профилю кулачка. Направлена она параллельно касательной t-t, что является условием непрерывности контакта кулачка и толкателя.
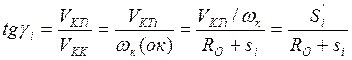 По построению имеем, что в
данном положении:
По построению имеем, что в
данном положении:
( 4.4 )
где RO – радиус базовой окружности кулачка, si – перемещение толкателя в данном положении, Si’ – значение передаточной функции в данном положении.
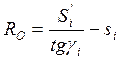 Выражение ( 4.4 ) показывает,
угол давления обратно пропорционален радиусу базовой окружности кулачка, т.е.
увеличивая RO
можно уменьшать g.
Выражение ( 4.4 ) показывает,
угол давления обратно пропорционален радиусу базовой окружности кулачка, т.е.
увеличивая RO
можно уменьшать g.
Разрешим выражение ( 4.4 ) относительно RO.
( 4.5 )
Если в правой части выражения ( 4.5 ) вместо текущего угла давления подставить его допускаемое значение, то в левой части получим минимально допустимый для данного положения радиус базовой окружности, т.е. такой при котором угол давления в данном положении механизма будет равен предельно допускаемому:
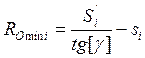 ( 4.6 )
( 4.6 )
Тогда минимальный радиус базовой окружности кулачка, обеспечивающий незаклинивание в любом положении механизма:
ROmin = max { ROmin i } ( 4.7 )
i
4.6.2. Механизм с толкателем при наличии эксцентриситета
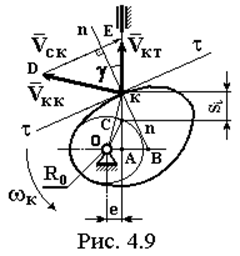 Расчетная схема для этого случая представлена на
рис. 4.9, где, как и в предыдущем случае n-n – нормаль к профилю кулачка в точке к контакта
кулачка и толкателя, t-t – касательная к профилю кулачка в этой же
точке, g – угол давления.
Механизм также изображен в некотором промежуточном положении на фазе удаления и
построен план скоростей механизма, на котором приняты те же обозначения VКТ, VКК, VСК, что и на рис. 4.8.
Расчетная схема для этого случая представлена на
рис. 4.9, где, как и в предыдущем случае n-n – нормаль к профилю кулачка в точке к контакта
кулачка и толкателя, t-t – касательная к профилю кулачка в этой же
точке, g – угол давления.
Механизм также изображен в некотором промежуточном положении на фазе удаления и
построен план скоростей механизма, на котором приняты те же обозначения VКТ, VКК, VСК, что и на рис. 4.8.
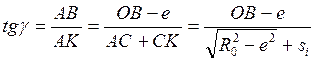 |
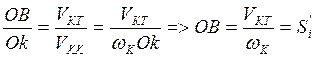 |
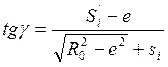 Таким образом, окончательно
Таким образом, окончательно
( 4.8 )
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.