При проектировании кулачкового механизма с роликом значение RP радиуса ролика может быть задано конструктором. В этом случае необходима проверка правильности выбранной величины. Если RP не задано, то эта величина рассчитывается на основе анализа кривизны профиля кулачка. Для нее должны удовлетворяться следующие неравенства [1, 9, 14]:
RP £ 0,7 rmin; RP £ 0,4 R O; ( 4.40 )
где rmin – минимальный радиус кривизны центрового профиля кулачка;
RO – радиус базовой окружности кулачка.
 В п. 4.8.1, 4.8.3 рассмотрен расчет координат профиля кулачка (Ri,
bi),
i = 1,2 … n. По этим величинам для каждых
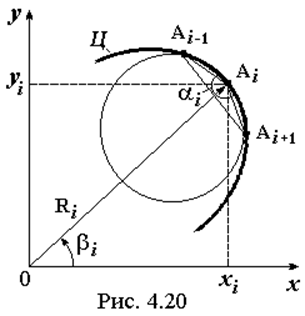
трех точек на центровом профиле кулачка Ai-1, Ai, Ai+1 (рис.
4.20) можно определить радиус описанной окружности ri, который
и будет приближенным значением радиуса кривизны центрового профиля в i-й
точке.
В п. 4.8.1, 4.8.3 рассмотрен расчет координат профиля кулачка (Ri,
bi),
i = 1,2 … n. По этим величинам для каждых
трех точек на центровом профиле кулачка Ai-1, Ai, Ai+1 (рис.
4.20) можно определить радиус описанной окружности ri, который
и будет приближенным значением радиуса кривизны центрового профиля в i-й
точке.
xi = Ri cos bi; yi = Ri sin bi. ( 4.41 )
Длины сторон треугольника Ai-1AiAi+1:
![]()
( 4.42 )
где k, j = i–1, i, i+1.
Решая треугольник Ai-1AiAi+1 получаем:
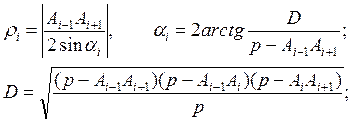
( 4.43 )
где p – полупериметр треугольника Ai-1AiAi+1.
rmin = min ri.
Если RP задан конструктором, то проверяются условия ( 4.40 ). Если он не задан или эти условия не выполняются, то конструктор, по известному теперь rmin из конструктивных соображений может принять любое значение RP в соответствии с условиями ( 4.40 ).
5.1. Классификация
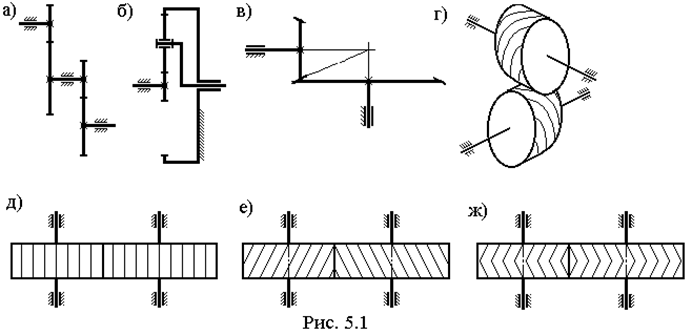 |
а) механизмы с неподвижными осями колес (рис. 5.1а,в,г,д,е,ж);
б) механизмы, в составе которых есть колеса с подвижными осями: планетарные (рис. 5.1б) и дифференциальные;
в) механизмы, в составе которых есть упруго деформируемые колеса (волновые).
2. По расположению осей колес:
а) механизмы с параллельными осями колес (цилиндрические рис. 5.1а,д,е,ж);
б) оси колес пересекаются (конические – рис. 5.1в);
в) оси колес скрещиваются (винтовые – рис. 5.1г, червячные, гипоидные).
3. По форме рабочей поверхности зуба:
а) эвольвентные;
б) циклоидальные;
в) часовое зацепление (приближенное на основе циклоидального);
г) зацепление Новикова;
д) цевочное зацепление.
4. По форме оси зуба: а) прямозубые (рис. 5.1д);
б) косозубые (рис. 5.1е);
в) шевронные (рис. 5.1ж);
г) винтовые (рис. 5.1г).
5.2. Основная теорема зацепления
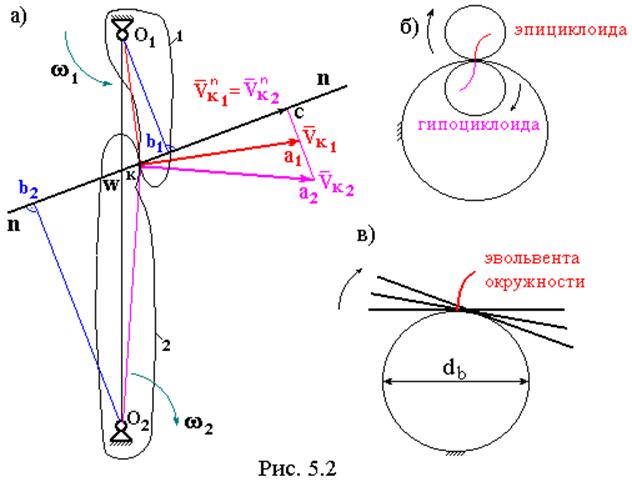
Основная теорема зацепления или теорема Виллиса формулируется следующим образом (рис. 5.2а). Общая нормаль к поверхностям двух вращающихся тел, проведенная в точке контакта отсекает от межцентрового расстояния отрезки, обратно пропорциональные угловым скоростям звеньев. То есть:
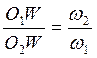 |
 |
 |
![]()
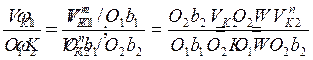 |
Последнее равенство в соотношениях ( 5.1 ) следует из подобия треугольников O1b1W µ O2b2W (см. рис. 5.2а). Теорема доказана.
Когда в процессе движения точка k проходит положение w, то в этот момент равны, не только нормальные, но и касательные составляющие скорости VК1t= VК2t, т.е. скорости полностью равны VК1 = VК2, поэтому точка w названа полюсом зацепления.
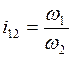 |
Как правило, при проектировании зубчатых механизмов требуется постоянное передаточное отношение.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.