Mg = Ma iag hag / nw ( 5.34 )
где nW – количество сателлитов.
5.9.2. Определение усилий в зацеплениях
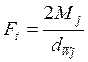 Вообще говоря, в зацеплении
действует одно усилие – это реакция в точке контакта зубьев R
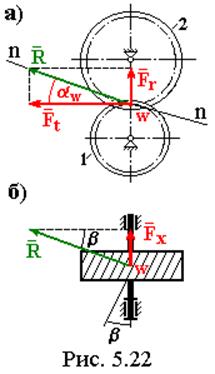
(рис. 5.22). Однако для расчетов удобнее использовать ее проекции. Окружное
усилие:
Вообще говоря, в зацеплении
действует одно усилие – это реакция в точке контакта зубьев R
(рис. 5.22). Однако для расчетов удобнее использовать ее проекции. Окружное
усилие:
( 5.35 )
где Mj – крутящий момент, действующий на данном колесе, dWj – диаметр начальной окружности колеса.
Радиальное усилие:
Fr = Ft tg aW ( 5.36 )
В косозубых и винтовых передачах возникает еще одно усилие – осевое (рис. 5.22б):
Fx = R sin b ( 5.37 )
где b – угол наклона зубьев.
Возникновение осевого усилия можно считать недостатком косозубых колес, т.к. оно воспринимается подшипниками вала и в этом случае необходимо хотя бы один подшипник делать радиально-упорным. Для преодоления этого недостатка применяют колеса с шевронными зубьями.
5.9.3. Определение реакций в опорах валов
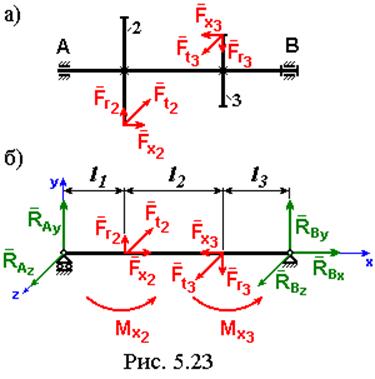
Эту задачу решим на примере второго вала механизма, изображенного на рис. 5.21. На рис. 5.23 представлены расчетные схемы. Разрываем кинематические пары зацепления колес 1-2 и 3-4 и в точках отсоединения прикладываем реакции отброшенных частей, которые в данном случае являются усилиями в зацеплениях (рис. 5.23а).
Приводя эти усилия к центрам колес, и полагая, что всю осевую нагрузку воспринимает подшипник B, получаем балку на двух опорах, нагруженную пространственной системой сил (рис. 5.23б).
Реакции в опорах A и B найдем из уравнений равновесия. Сначала найдем составляющие реакций, действующие в плоскости XY.
Из условия S FX = 0 получаем RBx = FX2 – F X3
Условие S MAXY = 0 дает:
RBy (l1+l2+l3) + Fr2 l1 – Fr3 (l1+l2) + MX2 + MX3 = 0.
Откуда: RBy = (Fr3 (l1+l2) – Fr2 l1 – MX2 – MX3) / (l1+l2+l3).
Тогда из условия S FY = 0 получаем:
RAy = Fr3 – Fr2 – RBy.
Теперь найдем составляющие реакций, действующие в плоскости XZ. Условие S MAXZ = 0 дает:
RBz (l1+l2+l3) – Ft2 l1 + Ft3 (l1+l2) = 0.
Откуда: RBz = (Ft2 l1 – Ft3 (l1+l2)) / (l1+l2+l3).
Тогда из условия S FZ = 0 получаем:
RAz = Ft2 – Ft3 – RBz.
5.10. КПД зубчатых механизмов
Подробный расчет КПД зубчатых механизмов не является задачей данного курса. Здесь мы рассмотрим лишь основные принципы. Более подробно этот вопрос рассмотрен, например, в работе [ 16 ].
Первое, что следует отметить – это то, что учет потерь на трение с помощью КПД представляет собой довольно грубую методику, применимую только для механизмов, имеющих достаточно высокую степень нагруженности внешними полезными силами, когда доля сил трения в общей силовой картине не высока. Это обычно характерно для машиностроения. В приборостроении, особенно в точном приборостроении, обычно применяют более тонкие методики.
5.10.1. КПД зубчатых механизмов с неподвижными осями колес
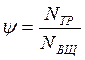 Введем понятие коэффициента потерь:
Введем понятие коэффициента потерь:
( 5.38 )
где NТР – мощность сил трения, NВЩ – мощность на ведущем колесе.
Тогда КПД механизма можно представить в виде
h = 1 – y ( 5.39 )
Общий коэффициент потерь механизма y находят как сумму коэффициентов потерь от различных видов потерь yi:
y = Syi
Рассмотрим основные виды потерь, характерные для зубчатых механизмов.
Потери на трение в зацеплениях обычно определяются по упрощенной эмпирической зависимости
yЗ » 2,3 f З (1/Z1 ± 1/Z2) ( 5.40 )
где f З » 1,25 f – коэффициент трения в зацеплении;
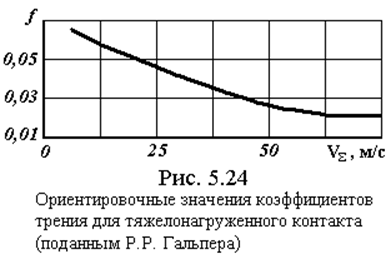
f – коэффициент трения скольжения, определяемый по номограммам, например, рис. 5.24 [16] в зависимости от степени нагруженности передачи и суммы скоростей контактирующих точек
VS » 2V sin aW,
V – окружная скорость зубчатых колес;
 |
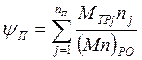 Потери на трение в подшипниках качения определяют
по формуле [ 16 ]
Потери на трение в подшипниках качения определяют
по формуле [ 16 ]
( 5.41 )
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.