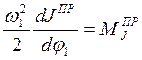Второе слагаемое – это момент, возникающий в том
случае, если приведенный момент инерции JПР
 |
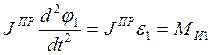( 7.17 )
Уравнение (7.16) является обыкновенным в общем случае нелинейным дифференциальным уравнением второго порядка с произвольной правой частью. В общем случае такое уравнение аналитического решения не имеет и, тогда, решается численно, например, одним из методов Рунге-Кутта.
Решением уравнения (7.16) являются функции: w1(t) и j1(t). Исключая t как параметр, можно получить функцию w1(j1) за цикл движения, например, за один оборот главного вала.
Однако выше была сформулирована задача не только моделирования движения, но и обеспечения требуемой плавности хода. Самый простой способ уменьшить коэффициент неравномерности хода – это установка маховика, который при разгоне машины аккумулирует кинетическую энергию, а при торможении отдает ее. Момент инерции маховика входит составной частью в JПР. Например, для машины рассмотренной в подразделе 7.1 общий приведенный момент инерции машины состоит из четырех частей:
JПР = JГМПР(j1) + JЗМПР + JРДПР + JМПР ( 7.18 )
где JГМПР(j1) – приведенный момент инерции главного механизма,
JЗМПР – приведенный момент инерции зубчатого механизма,
JРДПР – приведенный момент инерции ротора двигателя,
JМПР – приведенный момент инерции маховика.
В выражении (7.18) все слагаемые могут быть
определены так, как это описано в подразделе 7.4, кроме JМПР.
Его значение надо подобрать в процессе решения уравнения движения так, чтобы
выполнилось условие (7.3).
При моделировании установившегося режима работы возникает еще одна проблема – определение начальных условий.
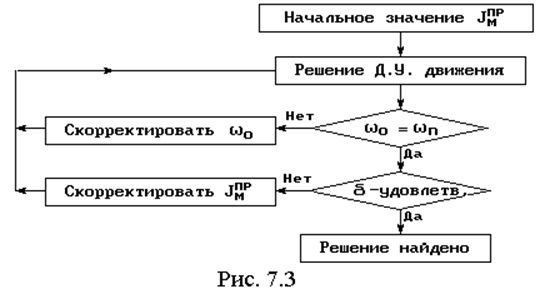
Обе этих задачи решаются с помощью алгоритма, представленного на рис. 7.3.
Для обеспечения требуемой плавности хода уравнение (7.16) решается многократно. При этом варьируется значение момента инерции маховика JМПР и контролируется стационарность режима работы. Процесс идет до тех пор, пока не будет найден вариант, удовлетворяющий заданному коэффициенту неравномерности хода.
В блок-схеме приняты обозначения: w0, wn – это значения w1 в начале и конце цикла.
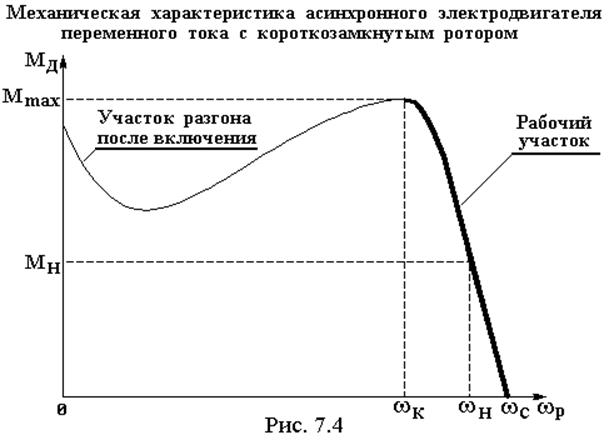
В качестве примера рассмотрим механический пресс, рассмотренный в подразделе 7.1 (см. рис. 7.1). Такие машины чаще всего имеют привод от асинхронного электродвигателя переменного тока. Момент, развиваемый такими двигателями, зависит от многих факторов, но в первом приближении его можно считать зависящим только от угловой скорости ротора. Вид статической механической характеристики асинхронного электродвигателя переменного тока представлен на рис. 7.4.
Характеристика состоит из двух участков. Тонкой линией показан характер изменения момента, развиваемого двигателем в процессе разгона сразу после включения. Рабочая часть характеристики расположена между значениями скорости ротора: wК – критическая скорость, wС – синхронная скорость. В этом промежутке находится wН – номинальная угловая скорость. В пределах рабочего участка асинхронные двигатели до некоторой степени обладают свойством саморегулирования, т.к. при разгоне ротора момент, развиваемый двигателем уменьшается, а при торможении – увеличивается. Но пределы этого довольно узки.
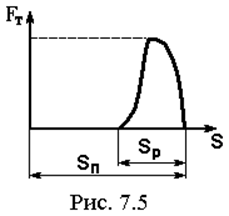
Характер изменения технологической силы FT, действующей на пуансон пресса, может быть различен. На рис. 7.5
показан один из возможных вариантов, где s – ход пуансона, sП – величина его полного хода, sР – величина рабочего хода.
На рис. 7.6 представлены решения дифференциального уравнения движения с подбором момента инерции маховика, т.е. результаты работы алгоритма показанного на рис. 7.3.
На рис. 7.6а – графики приведенных моментов, методика вычисления которых рассмотрена выше, где jН, jК – углы поворота кривошипа, соответствующие началу и концу технологической операции. На рис. 7.6б – результаты моделирования движения главного вала. На этой зависимости можно выделить шесть участков. Рассмотрим каждый из них.
Участок 1. Главный вал тормозится т.к. MДПР < MСПР + MJПР. MJПР на этом участке является моментом сопротивления.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.