Структурный анализ и синтез рычажных механизмов. Кинематический анализ рычажных механизмов. Динамика машин с упругими звеньями, страница 19

Нередко значение R_{О min},  полученное из условия ограничения угла давления, столь мало, что конструктивно не может быть реализовано. В этих случаях величины R_{О min,} е выбирают конструктивно, но так, чтобы центр вращения кулачка располагался в допустимой зоне. При этом, если оказывается, что выбранный R_О > R_{О min ц}, то целесообразно устанавливать е = 0, т.к. центральные механизмы более технологичны, а введение эксцентриситета разумно лишь тогда, когда позволяет уменьшить габариты.

4.7.2. Механизмы  с  плоским  толкателем

Схема такого механизма представлена на рис. 4.1,д. При работе этих механизмов угол давления в кинематической паре кулачок-толкатель всегда g = 0, поэтому заклинивание в этой кинематической паре им не грозит. Критерием же определения минимально допустимого радиуса базовой окружности кулачка является требование выпуклости профиля кулачка [14, 18], так как очевидно, что при наличии вогнутостей плоский толкатель не будет  их  отслеживать.

Математически условие выпуклости кулачка означает, его радиус кривизны в каждой точке должен быть положителен:

r > 0

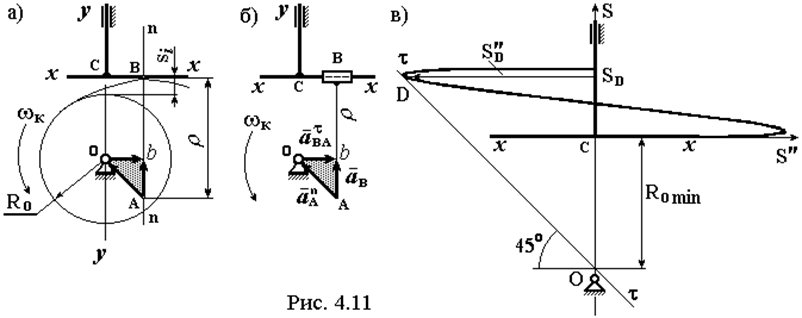
Найдем условия, при которых это будет выполняться. Проведем нормаль n-n в точке контакта толкателя с кулачком (рис. 4.11а). Пусть точка A является центром кривизны профиля. Как видно из рисунка

AB = r = R_O + s_i + Ab, где R_O – радиус базовой окружности кулачка, s_i – перемещение толкателя в данном положении, Ab – отрезок подлежащий определению.

Заменим высшую кинематическую пару на две низших, добавив фиктивное звено AB, как это показано на рис. 4.11,б. При этом получаем кулисный механизм. Построим для него план ускорений, соответствующий векторному уравнению:                                   _       _        _

a_B = a_Aⁿ + a_BO^t , где a_B = w_К S’’ = d²S/dt² – ускорение толкателя,

a_Aⁿ = w_К² r – нормальное ускорение точки A кулачка (r = OA),

a_BO^t – тангенциальное ускорение относительного движения (параллельно xx).

Построенный на плане механизма треугольник OAb подобен плану ускорений с полюсом в точке A. Следовательно, беря отношения соответствующих сторон, найдем:

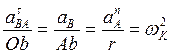Откуда искомый отрезок

где j – угол поворота кулачка, S” – аналог ускорения толкателя, по своему физическому смыслу это ускорение толкателя при единичной угловой скорости кулачка.

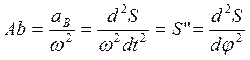Таким образом, радиус кривизны кулачка

r = R_O + s_i + S”.

И условие выпуклости кулачка:

r = R_O + s_i + S” ³ 0                                        ( 4.12 )

Поскольку R_O и s_i всегда положительны, то радиус кривизны может изменить знак только в том случае, если отрицательное значение аналога ускорения S” станет по абсолютной величине больше суммы R_O + s_i. Беря предельный случай, получаем, что условие выпуклости будет выполнено, если

R_O ³  – (s_i + S”) = – [s_i(j) + S”(j)]                        ( 4.13 )

Эта формула показывает, что наименьший допустимый радиус базовой окружности кулачка R_Omin определяется величинами перемещения толкателя s и аналога ускорения S”; решение надо искать в отрицательной зоне графика S”(j), для тех положений толкателя, в которых отрицательное отрицательное значение S” по абсолютной величине больше положительных значений s.

На рис. 4.11в показана диаграмма, с помощью которой можно найти величину R_O, такую, что профиль кулачка будет выпуклым. Здесь строится график функции S”(s), в одном масштабе по вертикальной оси откладывается перемещение s толкателя, а по горизонтальной – S”; это векторная величина, направление которой получают, повернув вектор скорости толкателя на 90^O в сторону, противоположную вращению кулачка.

Преобразуем неравенство ( 4.13 ):

R_O + s_i ³ –S”

или                                                 1 ³ S”/(R_O + s_i)

tg 45^O ³ S”/(R_O + s_i)

Проведем к отрицательной ветви кривой S”(S) касательную t-t под углом 45^О к оси S. Значение минимально допустимого радиуса базовой окружности кулачка  определится  выражением:

R_{o min} = (S”_D/tg 45^o) – S_D ;                                   ( 4.14 )