Одной из часто встречающихся задач является вопрос о существовании кривошипа, т.е. выяснение условий, при которых вращающееся входное звено сможет совершать полные обороты.
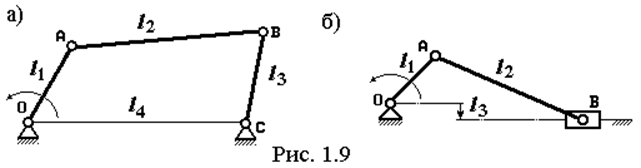
Из механизмов 2-го класса 2-го порядка эта задача чаще всего возникает для шарнирного четырехзвенника (рис.1.9а) и кривошипно-ползунного механизма (рис. 1.9б).
 |
– l1 + l2 + l3 – l4 > 0; – l1 + l2 – l3 + l4 > 0; – l1 – l2 + l3 + l4 > 0, ( 1.3 )
то механизм кривошипно-коромысловый (1 – кривошип, 3 – коромысло).
– l1 + l2 + l3 – l4 > 0; l1 + l2 – l3 – l4 > 0; l1 – l2 + l3 – l4 > 0, ( 1.4 )
или l1 = l3; l2 = l4, то механизм двухкривошипный (1, 3 – кривошипы).
У кривошипно-ползунного механизма (рис. 1.9б) звено 1 может совершать полные обороты только тогда, когда механизм можно провернуть. Проворачивание же механизма возможно только в том случае, когда угол давления[1] в шарнире между шатуном и ползуном не будет превышать 55О. Математически условие существования кривошипа у этого механизма:
l1 + l3 < 0,82 l2 ( 1.5 )
В выражении ( 1.5 ) величину смещения l3 надо брать с учетом знака. На рис. 1.9бэто смещение показано положительным.
Глава 2
Кинематический анализ рычажных механизмов
2.1. Постановка задачи
Если число степеней свободы механизма W = 1, то при фиксированных размерах звеньев значения их кинематических параметров движения однозначно определяются значениями кинематических параметров движения одного звена, называемого входным, которым и считается то звено, характер движения которого при кинематическом анализе полагается известным. Тогда задача кинематического анализа формулируется следующим образом: при известных мгновенных значениях кинематических параметров движения входного звена определить мгновенные значения кинематических параметров движения остальных звеньев. Таким образом, задача кинематического анализа решается автономно в каждом положении механизма, а для полного кинематического исследования ее надо решить многократно для ряда последовательных положений механизма за весь цикл его работы.
В дальнейшем при нумерации звеньев входное всегда будет иметь номер 1. Если оно совершает вращательное движение, то по условию задачи должны быть заданы: его угол поворота j01 от оси Хo неподвижной системы координат, угловая скорость w1, угловое ускорение e1. Если вращающееся входное звено совершает полные обороты, то его называют кривошипом. Часто его угол поворота удобно отсчитывать от того значения j01, которое соответствует какому-то характерному положению механизма, например, крайнему положению рабочего органа тогда будем обозначать его j1.
В результате решения задачи для звеньев, совершающих сложное движение (например шатуны), необходимо определить: а) поступательную составляющую движения, характеризуемую положением, скоростью и ускорением центра масс, б) вращательную составляющую, характеризуемую углом поворота, угловой скоростью и угловым ускорением. Для вращающихся звеньев достаточно определить их угол поворота, угловую скорость и угловое ускорение. Для поступательно движущихся звеньев – положение интересующей нас точки, например, центра масс и его линейную скорость и ускорение.
Решение описанной задачи опирается на структурный анализ механизма. Общую последовательность кинематического расчета можно представить следующим образом. По исходно заданным кинематическим параметрам движения входного звена определяются параметры движения той его точки, в которой присоединяется первая структурная группа. Производятся расчеты для нее и вычисляются параметры движения той точки звена структурной группы, в которой присоединяется следующая. Эти значения преобразуются в систему координат следующей структурной группы, производится ее расчет и т.д.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.