– m p2D2 – h p D1 + C D2 = 0
Сгруппируем слагаемые при D1 и D2
(С – mp2 )D1 + hpD2 = F0
– h p D1 + (С – mp2) D2 = 0
Отсюда получаем выражения для D1иD2:
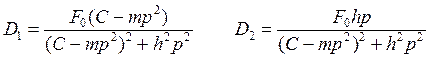 |
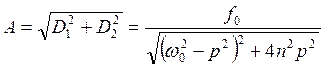
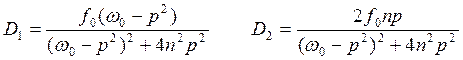 |
( 8.21 )
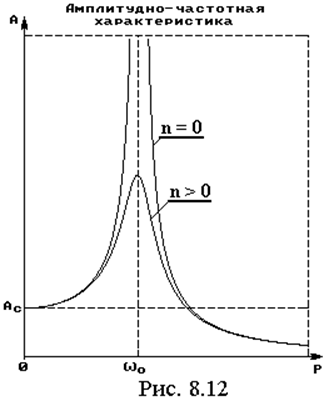
Выражение ( 8.21 ) можно рассматривать как функцию от частоты воздействия: A = f(p). График этой функции, называемой амплитудно-частотной характеристикой (АЧХ) представлен на рис. 8.12. При p = 0 имеет место статическая деформация:
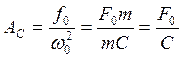
Когда частота вынуждающей силы совпадает с частотой собственных колебаний p = w0 – имеет место резонанс. В этой ситуации при отсутствии демпфирования (n = 0) знаменатель выражения ( 8.21 ) обращается в ноль и амплитуда колебаний равна бесконечности, но это чисто теоретический случай. В реальных случаях всегда есть демпфирование (n > 0) и амплитуда колебаний хоть и не бесконечна, но достигает в этой точке максимума, что может быть весьма опасно. При дальнейшем увеличении частоты вынуждающей силы амплитуда колебаний уменьшается, в пределе – до нуля.
8.7.3. Коэффициент виброизоляции
Рассмотренная выше амплитудно-частотная
характеристика дает качественное и количественное представление о зависимости
амплитуды колебаний от частоты вынуждающей силы, но не дает критерия для
проектирования амортизирующей подвески оборудования. Такой критерий дает
коэффициент виброизоляции.
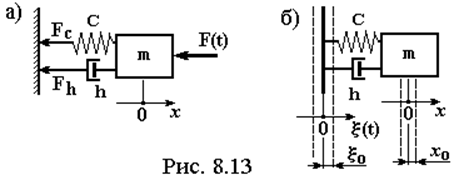
По определению коэффициент виброизоляции (kB) при силовом воздействии (рис. 8.13а) это отношение амплитуды силы, передаваемой на основание к амплитуде внешней силы:
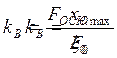
По определению коэффициент виброизоляции
при кинематическом воздействии (рис. 8.13б) это отношение амплитуды колебаний
объекта к амплитуде колебаний основания:
Таким образом, коэффициент виброизоляции характеризует эффективность амортизирующей подвески. Она эффективна, если kB < 1.
Найдем выражение для коэффициента виброизоляции при силовом воздействии. Рассмотрим уравнение ( 8.18 ). Соответствующее ему приведенное уравнение:
![]() + 2n
+ 2n![]() + w02x = f0cospt
+ w02x = f0cospt
где f0 = F0 /m.
Решение этого уравнения для установившихся колебаний имеет вид:
x(t) = A cos(pt + a); ![]() (t) = - pA sin(pt+ a)
(t) = - pA sin(pt+ a)
Сила, передающаяся на основание состоит из двух компонент: сила от упругой связи FC(t) и сила от демпфирующей связи Fh(t)
FOCH = FC(t)
+ Fh(t) = С x(t) + h ![]() (t)= C A cos(pt + a) – h pA sin(pt+ a)
(t)= C A cos(pt + a) – h pA sin(pt+ a)
С другой стороны, амплитуду колебаний объекта можно выразить из формулы ( 8.21 )
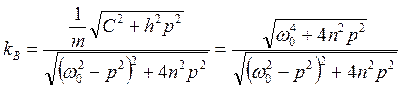
( 8.22 )
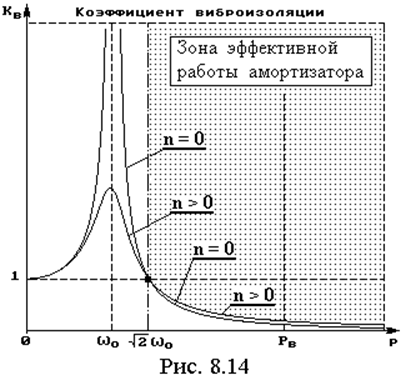 |
Таким образом, по характеру зависимости kB(p) можно отметить следующие особенности:
1. Амортизирующая подвеска эффективна только тогда,
когда частота вынуждающей силы оказывается правее (больше) частоты ![]() w0.
w0.
2. Увеличение демпфирования в рабочей зоне амортизатора ухудшает эффект амортизации, т.е. увеличивает амплитуду колебаний, но в зоне резонанса заметно уменьшает амплитуду.
8.7.4. Основные принципы проектирования амортизирующей подвески
Прежде всего, следует проанализировать внешние
воздействия, которым будет подвергаться защищаемый объект. Определить спектры
этих воздействий и выделить наименьшую частоту. Вот эта то, наименьшая
характерная, частота внешнего воздействия pB
и должна быть больше ![]() w0.
w0.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.