Структурный анализ и синтез рычажных механизмов. Кинематический анализ рычажных механизмов. Динамика машин с упругими звеньями, страница 6

В соответствии с описанным алгоритмом строится и дальнейшее изложение. Сначала будет рассмотрена кинематика входных механизмов, а после этого  расчет структурных групп, для которых уже можно будет полагать, что параметры движения входных кинематических пар известны. Основные расчетные  зависимости  для  структурных  групп  получим  методом  векторных  контуров [ 5, 9, 14, 18 ], параметры движения характерных точек на звеньях, таких как центры масс,  рабочий  орган  и т.п. – методом  преобразования  координат.

Расчетные  зависимости  для  определения  кинематических  параметров движения  звеньев  будут получены  для  структурных  групп  2 класса  2  порядка.  При  этом  итоговые  выражения  в  качестве необходимых исходных данных  будут  содержать  параметры  движения   входных  кинематических пар.  Это  позволяет  использовать  полученные  зависимости  для  расчета механизмов,  содержащих  несколько  структурных  групп  и  при  различных  видах  движения  входного  звена.

Все методики расчетов реализованы в виде пакетов прикладных программ. В соответствии с этим ниже рассматриваются два варианта решения  задачи кинематики. Первый упрощенный, ориентированный на пакет TMM_KP,  когда  одна  из  внешних  кинематических пар  структурной группы связывает  соответcтвующее звено со стойкой. Второй общий, реализованный в пакетах PRIAM и SIKAM, когда группа обеими внешними кинематическими парами  может  присоединяется  к  подвижным  звеньям.

2.2. Кинематика  входных  механизмов

2.2.1 Кривошип

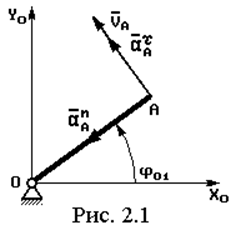Термин “кривошип” здесь применяется для краткости. Рассматривается любое вращающееся звено, имеющее кинематическую пару со стойкой (рис. 2.1). Координаты точки А конца кривошипа в неподвижной системе  Xo,Yo:

x_A = l_ОА cos j₀₁ , y_A = l_ОА sin j₀₁

где l_ОА  – длина  кривошипа.

Скорость точки  А:    V_A = w₁ l_ОА, а  ее  проекции:          V_Ax = – w₁ l_ОА sin j₀₁, 

V_Ay = w₁ l_ОА cos j₀₁ .

Ускорение точки А имеет две составляющие: нормальную, характеризующую изменение вектора скорости по направлению и касательную, характеризующую  изменение  вектора  скорости  по  величине:

_      _      _

a_Aⁿ  =  w₁² l_OA ,   a_A^t  =  e₁ l_OA ,   a_A  =  a_Aⁿ ₊ a_A^t .

Проекции  составляющих  ускорения,  соответственно

a_Axⁿ = – w₁² l_OA cos j₀₁ ,  a_Ayⁿ = – w₁² l_OA sin j₀₁ ,

a_Ax^t = – e₁ l_OA sin j₀₁ ,     a_Ay^t = e₁ l_OA cos j₀₁ .

2.3.  Аналитические  зависимости  кинематического  анализа

для  структурных  групп,  связанных  со  стойкой

Решать задачу кинематического анализа будем методом векторных контуров, суть которого состоит в следующем. Звенья механизма представляют в виде векторов. Поскольку в данном случае механизм замкнут через стойку, то эти векторы образуют замкнутые контуры. Записывают уравнения замкнутости векторных контуров. Выбирают удобную систему координат и на её оси проецируют уравнения замкнутости, получая тем самым системы уравнений для определения параметров, характеризующих положения звеньев. Далее эти системы уравнений последовательно дважды дифференцируют по времени, получая системы уравнения соответственно для вычисления скоростей и ускорений.

Рассматриваться будут механизмы с входным звеном – кривошипом, но это никак не ограничивает общности, т.к. в итоговых выражениях входными кинематическими параметрами будут параметры движения входной кинематической пары и полученные результаты будут инвариантны по отношению к входному движению.

Описанная  здесь  методика  используется  в  пакете  ТММ_КР.

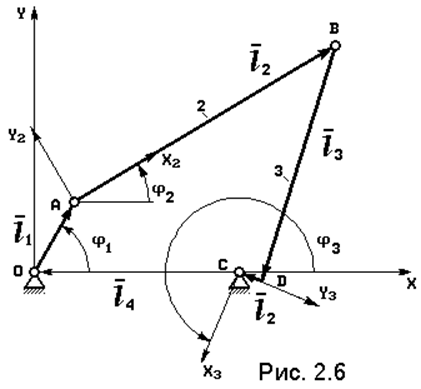
2.3.1. Трехшарнирная  структурная  группа

Механизм, состоящий из входного звена OA и структурной группы с тремя вращательными кинематическими парами представлен на рис. 2.6. Механизм может иметь две сборки (рис. 2.7, 2.8). Сборку, показанную на рис. 2.6, 2.7, принято считать прямой, а сборку на рис. 2.8 – обратной. В общем случае ось коромысла ВС может быть  смещена от точки C на величину CD (рис. 2.6). Сначала найдем решение для случая CD  = 0 (см. рис. 2.7, 2.8). Все величины, помеченные ниже знаком “*” относятся к этому  случаю.