Структурный анализ и синтез рычажных механизмов. Кинематический анализ рычажных механизмов. Динамика машин с упругими звеньями, страница 39

Таким образом, цель исследования предварительно можно сформулировать как задачу математического моделирования движения главного вала машины под действием приложенных машинному агрегату сил и моментов с помощью уравнения движения. Результатом моделирования, т.е. решения данного уравнения, будет искомый закон движения  главного  вала  за  один  оборот:

w₁ = f(j₁),                                           ( 7.1 )

где  j₁ – угол  поворота  главного  вала,   w₁ – его  угловая  скорость.

К машинам, работающим в установившемся режиме, например, к технологическим машинам обычно предъявляют определенные требования по плавности хода. В частности на рис. 7.1 изображена схема механического пресса. У такой машины слишком большое торможение в процессе технологической операции может привести к снижению качества изготавливаемых деталей.

По функции (7.1) можно установить максимальное w_max и минимальное w_min значение угловой скорости. По этим данным вычисляется коэффициент  неравномерности  хода

d = 2 (w_max – w_min)/( w_max + w_min ),                           ( 7.2 )

являющийся количественной характеристикой степени отклонения угловой скорости от среднего значения. При проектировании машины, работающей в циклическом режиме обычно задается предельно допустимое значениекоэффициента неравномерности хода [ d ], и в конечном итоге  должно  выполняться  условие:

d_факт £ [ d ]                                             ( 7.3 )

Если в результате моделирования окажется, что условие ( 7.3 ) не выполняется, то на главный вал машины необходимо установить маховик, момент инерции которого должен быть подобран так, чтобы ( 7.3 ) выполнилось.

Резюмируя, можно окончательно сформулировать цели исследования как математическое моделирование движения главного вала машины и обеспечение на этой основе заданной плавности хода путем подбора требуемой маховой  массы.

7.2. Метод  приведения

Решать задачу будем методом приведения, суть которого сводится к следующему. Звено, характер движения которого будет исследоваться, выбирается в качестве звена приведения. К этому звену приводится вся внешняя нагрузка, действующая на все звенья машины. К этому же звену приводятся все инерционные свойства всех звеньев.

В данном случае, для машины, изображенной на рис. 7.1 звеном приведения будет главный вал машины – вал кривошипа главного механизма. Поскольку в этом случае звено приведение совершает вращательное движение, то внешняя нагрузка к нему будет приведена в виде так называемого приведенного момента M^ПР, а инерционные параметры – в виде приведенного момента инерции – J^ПР.

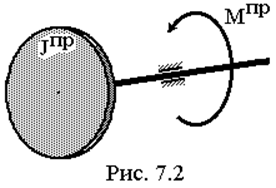Таким образом, реальный машинный агрегат заменяется эквивалентной динамической моделью – рис. 7.2. Для этой модели составляется уравнение движения, решение которого и является моделированием движения.

7.3. Приведение  сил  и  моментов

Задача состоит в том, чтобы найти такой приведенный момент M^ПР, приложенный к звену приведения, который эквивалентным образом заменял бы собой воздействие всех внешних сил и моментов, действующих на все звенья машины.

В общем случае на каждое звено может действовать несколько внешних сил и моментов, но существует теорема, о том, что любая система сил, действующих на тело, может быть приведена к одной силе, приложенной в центре масс тела и моменту относительно центра масс. Эту силу и момент называют главным вектором и главным моментом сил, действующих на тело. Будем полагать, что этот этап приведения предварительно выполнен.

Условием приведения внешних сил к звену приведения является равенство мощностей, развиваемых реальными силами и моментами, приложенными к звеньям и мощности, развиваемой приведенным моментом на звене приведения, т.е.:

N^ПР = N_S                                                     ( 7.4 )

Раскрывая выражения для мощностей, имеем:

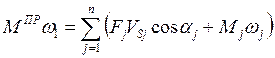
( 7.5 )

где F_j, M_j – главные векторы и главные моменты сил, приложенных к звеньям,

V_Sj  – скорости центров масс звеньев,

a_j  – углы между векторами F_j и V_Sj,

w_j  – угловые скорости звеньев,

n – количество подвижных звеньев в машине.